500 câu trắc nghiệm cuối HK1 Toán 8 - CTST - Đề 1
21 câu hỏi 60 phút
Đa thức \(A=x^2+2y^5−x^4y^4−1\) có bao nhiêu hạng tử?
3
4
5
6
Đa thức \(A=x^2+2 y^5-x^4 y^4-1\) có 4 hạng tử là: \(x^2 ; 2 y^5 ;-x^4 y^4 ;-1\).
Danh sách câu hỏi:
Đa thức \(A=x^2+2 y^5-x^4 y^4-1\) có 4 hạng tử là: \(x^2 ; 2 y^5 ;-x^4 y^4 ;-1\).
Hai đơn thức thu gọn là \(A=(0,3+\pi) x^2 y ; D=(\sqrt{2}+1) x y^2 z\) vì hai đơn thức này là dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.
\((x+y)^2=x^2+2 x y+y^2\) (bình phương của một tổng)
\((x+y)^3=x^3+3 x^2 y+3 x y^2+y^3\) (lập phương của một tổng)
\(x^3-y^3=(x-y)\left(x^2+x y+y^2\right)\) (hiệu hai lập phương)
\( (x-y)^3=x^3-3 x^2 y+3 x y^2-y^3 \) (lập phương của một hiệu)
Biểu thức \(\frac{x}{0}\) không phải phân thức vì mẫu thức là đa thức không.
Biểu thức \(\frac{x+y}{\frac{1}{y}}\) và \(\frac{1}{\frac{x^2-y^2}{x y}}\) không phải là phân thức thì mẫu thức không phải là đa thức.
Biểu thức \(\frac{x^2+y}{\frac{1}{2} y}\) là đa thức vì \(x^2+y\) và \(\frac{1}{2} y\) đều là đa thức khác đa thức 0.
Hình chóp tam giác đều có 4 mặt, 6 cạnh.
Hình chóp tứ giác đều có 5 đỉnh, đáy là hình vuông.
Câu 6:
Một hình chóp tứ giác đều có cạnh đáy là a và độ dài trung đoạn là b thì có diện tích xung quanh là
Câu 11:
Cho biểu đồ sau:
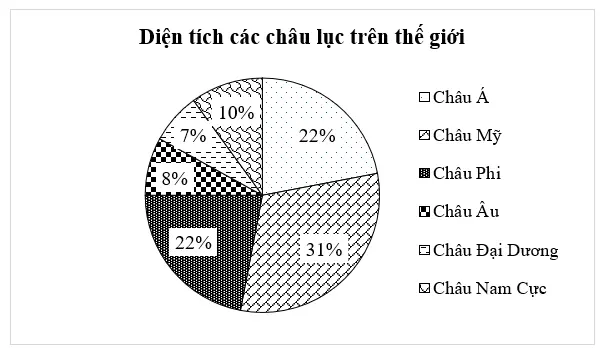
Hỏi châu Mỹ chiếm bao nhiêu phần trăm tổng diện tích của cả sau châu lục đó?
Câu 13:
Cho hai đa thức: \(R=\left(x y-4 x^2+2\right) \cdot x y^2\) và \(T=\left(15 x^3 y^4-20 x^4 y^3+10 x^2 y^3\right): 5 x y\).
Đa thức \(S\) thỏa mãn \(R=T-S\)
Hệ số tự do của đa thức \(R\) là 2
Bậc của đa thức \(T\) là 3
Giá trị của biểu thức \(T\) tại \(x=1 ; y=-1\) là -5
\(S\) là một đơn thức
Câu 14:
Cho tam giác nhọn \(A B C\) có \(A B<B C\). Từ trung điểm \(M\) của cạnh \(A B\) kẻ đường thẳng song song với \(B C\) cắt cạnh \(A C\) tại \(N\). Trên cạnh \(B C\) lấy điểm \(D\) sao cho \(B D=M N\). Kẻ đường cao \(A H(H \in B C)\) của tam giác \(A B C\)
Tứ giác \(B M N D\) là hình bình hành
Tam giác \(A M H\) cân tại \(A\)
\(\widehat{A M N}=\frac{2}{3} \widehat{H M N}\)
Tứ giác \(D H M N\) là hình thang cân