10 Đề thi kiểm tra giữa HK1 môn Toán lớp 7 - CTST - Đề 3
18 câu hỏi 60 phút
Cách viết nào sau đây biểu diễn một số hữu tỉ?
\(\frac{{6,5}}{{14}}.\)
\(\frac{3}{7}.\)
\(\frac{{21}}{0}.\)
\(\frac{{15}}{{0,2}}.\)
Số hữu tỉ là số được viết dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Do đó, \(\frac{3}{7}\) biểu diễn một số hữu tỉ.
Danh sách câu hỏi:
Số hữu tỉ là số được viết dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Do đó, \(\frac{3}{7}\) biểu diễn một số hữu tỉ.
Nhận thấy, \(a;b\) đều nằm bên phải so với số \(0\) và \(b\) nằm gần số \(0\) hơn \(a.\)
Do đó, ta có: \(0 < b < a.\)
Ta có: \({\left( { - \frac{1}{2}} \right)^3} = \frac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}} = \frac{{ - 1}}{8}.\)
Câu 4:
Thực hiện bỏ ngoặc của phép tính \( - \left( {a + 2} \right) + \left( {b - 2} \right)\) ta được
Ta có: \( - \left( {a + 2} \right) + \left( {b - 2} \right) = - a - 2 + b - 2 = - a + b + \left( { - 2 - 2} \right) = - a + b - 4\).
Số vô tỉ là số được viết dưới dạng số thập phân vô hạn không tuần hoàn.
Do đó, số vô tỉ là \(0,010010001...\)
Câu 9:
Diện tích xung quanh của một hình lăng trụ đứng tứ giác có chu vi đáy là \(C\) và chiều cao \(h\) là
Câu 13:
Cho lăng trụ đứng tứ giác có đáy là hình thang cân như hình vẽ bên.
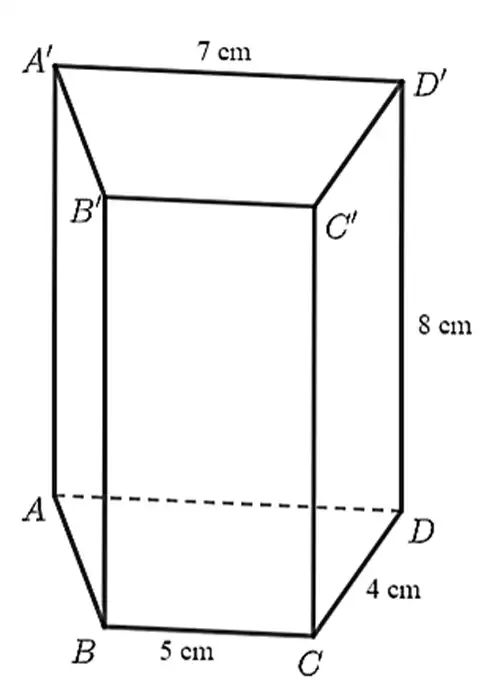
Các mặt đáy của hình lăng trụ là \(ABCD\) và \(A'B'C'D'.\)
\(AB = CD = 4{\rm{ cm}}{\rm{.}}\)
Chu vi đáy của hình lăng trụ đứng bằng \(24{\rm{ cm}}{\rm{.}}\)
Diện tích xung quanh của hình lăng trụ đứng bằng \(160{\rm{ c}}{{\rm{m}}^2}{\rm{.}}\)
Câu 14:
Người thứ nhất đi xe đạp từ \(A\) đến \(B\) hết \(6\) giờ; người thứ hai đi xe máy từ \(B\) về \(A\) hết \(3\) giờ; người thứ hai khởi hành sau người thứ nhất \(2\) giờ
Sau một giờ người thứ hai đi được \(\frac{1}{3}\) quãng đường
Sau một giờ người thứ nhất đi được \(\frac{1}{6}\) quãng đường
Sau khi người thứ hai đi được 1 giờ thì cả hai người đi được \(\frac{1}{2}\) quãng đường
Sau khi người thứ hai đi được 1 giờ thì hai người gặp nhau