Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(M\left( {1;2; - 2} \right)\) và mặt phẳng \(\left( P \right)\) có phương trình \(2x + y - 3z + 1 = 0\). Phương trình đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) là     

Mark the letter A, B, C, or D to indicate the word that differs from the other three in the position of primary stress in each of the following questions.

Phân tử S₈ có 128 electron, hỏi số hiệu nguyên tử của lưu huỳnh (S) là bao nhiêu?

(1) Tiền thân của cái bát có lẽ do con người dùng vỏ hoa quả như vỏ quả dừa và vỏ trai, sò để đựng thức ăn, sau đó có thể làm những chiếc bát bằng gỗ, cuối cùng cái bát ra đời [...]. Cái bát thuyền trong các mộ thời Hán có dạng như một lòng bàn tay, có hai cạnh để cầm và nó cũng giống như hình một chiếc thuyền thúng. Tuy nhiên, trừ cái bát thuyền ra, mọi cái bát khác đều có thể tích cơ bản là hai lòng bàn tay chụm lại, mà con người đã từng làm như thế để uống nướĐó chính là chiếc bát ăn cơm thông thường ngày nay. Song, hình như con người lại không ưa một sự mô phỏng thuần tuý như thế, những chiếc bát men đen, men ngọc thời Lý và những chiếc bát đàn thời Hậu Lê lại có dạng loe miệng và thót đáy như một cái nón, khả năng vuốt bàn xoay hình nón cũng dễ hơn vuốt hình tròn cong đều từ chân lên thành. Cái bát cong đều như thế có trong gốm hoa lam thời Trần và chúng có chân rất cao. Một cải tiến nữa kết hợp giữa bát hình nón và bát chân cao sinh ra cái bát chiết yêu duyên dáng thế kỉ XVIII – XIX.

(2) Đồ gốm gia dụng thời Lý – Trần quá thanh nhã khiến chúng ta không thể tưởng tượng rằng có thời con người sống cao sang như thế, nếu như đồ gốm phản ánh sự sử dụng và món ăn chúng chứa đựng. Những chiếc chậu, những chiếc âu mà hôm nay chúng ta nâng niu như cổ vật quý hiếm thì ngày xưa chúng chỉ được để rửa ráy chân tay mà thôi. Ở nông thôn, những gia đình trung bình đều có một chạn bát đĩa thường dụng và một vài rổ bát đĩa cất trong buồng dùng khi có cỗ bàn. Bát ăn cơm, bát chiết yêu, ang và âu, đĩa lòng nông vài cỡ, đũa cả, đũa ăn, muôi bằng gỗ, còn thìa thì hầu như không có, và thế là đủ cho một bữa ăn gia đình, tối bắc chống nhỏ ra sân đặt mâm cơm lên, mọi người ngồi xung quanh bằng ghế đẩu. Những đồ gốm này thường có men trắng đục, trắng xanh, ít hoa văn, mỏng manh, dễ vỡ, cấu tạo đơn sơ, chất lượng đất không tỉnh, nhưng giá rẻ. [...] Ngay từ cuối thời Trần, làng Bát Tràng đã sản xuất những loại gốm gia dụng men lam như thế, một số đồ đẹp dâng cho triều đình, còn lại, bán ra cho dân. Từ sau thế kỉ XV, xu hướng đồ dân gian và cung đình ngày càng tách biệt, thậm chí triều đình còn mở những lò riêng hoặc đặt những lô hàng riêng có đề chữ Nội phủ, hơn nữa là sang Trung Hoa đặt mua đồ gốm sứ cho hoàng triều. [...] Dân thành thị cũng có xu hướng dùng đồ gốm gia dụng Trung Hoa và Nội phủ, tạo ra sự phân biệt giữa nông thôn và thành thị trong thị trường đồ gốm. 

(Phan Cẩm Thượng, Đồ gốm gia dụng của người Việt, in trong Văn minh vật chất của người Việt, NXB Thế giới, Hà Nội, 2018)

Từ sau thế kỉ thứ XV, dân nông thôn có xu hướng sử dụng đồ gốm như thế nào?

Bảng số liệu dưới đây biểu thị khối lượng, đơn giá và đơn giá trung bình của một số loại thực phẩm mà siêu thị mini nọ bán được trong 3 ngày liên tiếp: ngày thứ nhất, ngày thứ hai và ngày thứ ba.

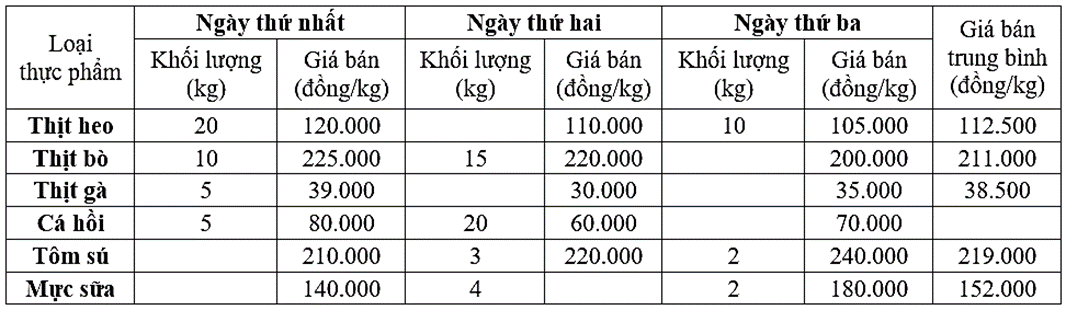
Biết trong 3 ngày này:

 Tổng khối lượng thịt heo bán được gấp đôi tổng khối lượng cá hồi bán được.

 Tổng khối lượng thịt bò bán được nhiều hơn tổng khối lượng thịt gà bán được là 20kg.

 Tổng khối lượng tôm sú bán được bằng tổng khối lượng mực sữa bán được.

Giá bán trung bình của mỗi kilogam cá hồi là

Một bánh xe quay đều 100 vòng trong 2s. Chu kì quay của bánh xe là

Read the following passage and mark the letter A, B, C, or D on your answer sheet to indicate the correct word or phrase that best fits each of the numbered blanks from 26 to 30.

We all had the experience of trying to learn something new only to find out that we're not very good at it. We look around at (26) _______ people we are learning with, those seemingly more gifted than us. It seems to come naturally to them.

Undoubtedly, there are people (27) _______ are brilliant at certain things. (28) _______ , many of them are not really born with talents. Psychologist K. Andrers Ericsson studied students at Berlin's Academy of Music. He found that while all the participants in the study had all the (29) _______ of world famous musicians, only some of them actually reached international stardom. What made the difference? The answer is simple: practice. The people that became (30) _______ were more competitive and practised about 2,000 hours more than others. It turns out that practice really does make perfect.

(Adapted from Empower)

The answer of question 29:

Đâu là cơ quan hành pháp của nước ta?

Khi bị đứt tay, sẽ có những hệ nào tham gia để bảo vệ cơ thể?

The government will get city dwellers________ 20% of their carbon footprint.

“Về quan hệ giữa đổi mới kinh tế và đổi mới chính trị, phải tập trung làm tốt đổi mới kinh tế, đáp ứng những đòi hỏi cấp bách của nhân dân về đời sống, việc làm và các nhu cầu xã hội khác, xây dựng cơ sở vật chất – kĩ thuật của chủ nghĩa xã hội, coi đó là điều kiện quan trọng để tiến hành thuận lợi đổi mới trong lĩnh vực chính trị. Đồng thời đổi mới kinh tế phải từng bước đổi mới tổ chức và phương thức hoạt động của hệ thống chính trị, phát huy ngày càng tốt quyền làm chủ và năng lực sáng tạo của nhân dân trên các lĩnh vực chính trị, kinh tế, văn hóa, xã hội”.

(Đảng Cộng sản Việt Nam, Văn kiện Đại hội đại biểu toàn quốc lần thứ VII, NXB Sự thật, Hà Nội, 1991, tr.54)

Nội dung nào sau đây phản ánh đúng về đổi mới chính trị của Đảng Cộng sản Việt Nam?

Cho bảng số liệu sau:

Số doanh nghiệp đăng ký thành lập mới phân theo ngành kinh tế giai đoạn 2016 - 2022

(Đơn vị: doanh nghiệp)

(Nguồn: Tổng cục Thống kê)

Trong giai đoạn 2016 - 2022, tỉ trọng số lượng doanh nghiệp đăng kí thành lập mới của ngành dịch vụ tăng bao nhiêu %? (Làm tròn kết quả đến số thập phân thứ nhất của %)

Trả lời:

Hệ thống lái bên phải được phân loại căn cứ vào:

Hiện tượng biến tính protein là hiện tượng gì?

Nội dung nào sau đây không phải thuế trực thu?

Thực vật C₄ thích nghi với điều kiện môi trường (hàm lượng CO₂ thấp) bằng cách

Nhờ các dịch vụ kết nối nhà tuyển dụng và người lao động, thị trường việc làm giúp cho thị trường lao động nhanh chóng đạt đến trạng thái nào?