Trong không gian \(Oxyz\), cho điểm \(A\left( -5;2;3 \right)\) và \(B\) là điểm đối xứng của \(A\) qua trục \(Oy\). Độ dài đoạn thẳng \(AB\) bằng:
Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 – Môn Toán – Bộ Đề 01 do cụm trường tỉnh Đồng Nai biên soạn là tài liệu ôn luyện hữu ích dành cho học sinh lớp 12 đang chuẩn bị cho kỳ thi tốt nghiệp THPT. Đề thi được xây dựng bám sát theo cấu trúc và mức độ của đề minh họa do Bộ Giáo dục và Đào tạo công bố, bao gồm đầy đủ các dạng câu hỏi từ nhận biết, thông hiểu đến vận dụng và vận dụng cao. Tài liệu không chỉ giúp học sinh rèn luyện kỹ năng làm bài mà còn hỗ trợ giáo viên trong công tác giảng dạy và đánh giá năng lực học sinh một cách hiệu quả.
Câu hỏi liên quan
Cho hình hộp \(ABCD.A'B'C'D'\). Đẳng thức nào sau đây là đẳng thức đúng?
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,SA=a\sqrt{3}\), đường thẳng \(SA\) vuông góc với mặt phẳng (\(ABCD\)) (tham khảo hình vẽ).
Tổng \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{SA}\) bằng:
Một sân vận động với sân bóng phẳng hình chữ nhật có chấm trắng trung tâm là nơi giao bóng, một đường kẻ vạch chia đôi sân và các khán đài. Khán đài A gồm những dãy ghế nằm vuông góc với vạch chia đôi sân có độ cao tăng dần (các ghế cùng hàng thì cùng độ cao so với mặt sân). Chọn hệ trục tọa độ \(Oxyz\) sao cho \(O\) trùng với điểm giao bóng, mặt phẳng \(Oxy\) trùng với mặt sân, trục \(Ox\) trùng với vạch chia đôi sân, tia \(Oz\) vuông góc với mặt sân (đơn vị đo lấy theo mét).
Một khán giả ngồi tại vị trí \(M\) của khán đài A, có hình chiếu vuông góc lên mặt phẳng chứa sân là một điểm thuộc \(Ox.\) Góc hợp bởi \(OM\) và mặt sân là \(\alpha \) với \(\sin \alpha =\frac{1}{3},\) nếu người này di chuyển 10 (m) trên hàng ngang đó đến ngồi tại một vị trí \(N\) thì góc hợp bởi \(ON\) và mặt sân là \(\beta \) với \(\sin \beta =\frac{\sqrt{10}}{10}.\) Gọi \(h~\left( m \right)\) là độ cao tại \(M\) so với mặt sân.
Một chiếc máy quay phim có trọng lượng \(300N\) được đặt trên một giá đỡ ba chân với điểm đặt \(E\left( 0;0;6 \right)\) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là:
\({{A}_{1}}\left( 0;1;0 \right)\), \({{A}_{2}}\left( \frac{\sqrt{3}}{2};-\frac{1}{2};0 \right)\), \({{A}_{3}}\left( -\frac{\sqrt{3}}{2};-\frac{1}{2};0 \right)\) (Hình bên dưới).
Giả sử \(\overrightarrow{{{F}_{1}}}=\left( a,b,c \right)\) khi đó \(a+3b-c\) bằng:
Một khinh khí cầu ở toạ độ \(A\left( -16;-10;10 \right)\) bắt đầu bay với véc tơ vận tốc không đổi \(\overrightarrow{v}\left( 4;3;-1 \right)\) (đơn vị vận tốc là km/h) và dự kiến bay trong thời gian 10 giờ. Biết trạm kiểm soát không lưu được đặt ở vị trí gốc toạ độ \(O\) kiểm soát được các vật thể cách trạm một khoảng tối đa bằng \(12\) km. Trạm kiểm soát không lưu có thể quan sát được sự di chuyển của khinh khí cầu trong khoảng thời gian bao nhiêu phút?
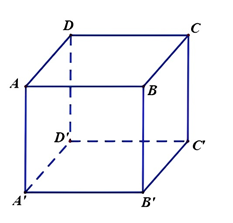
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Mệnh đề nào sau đây sai?
Cho hình hộp \(ABCD\cdot {A}'{B}'{C}'{D}'\). Chọn đẳng thức vectơ đúng:
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\). Độ dài của vectơ \(\vec{u}=\overline{{A}'{C}'}-\overline{{A}'A}\) bằng:
Trong không gian, cho hình hộp \(ABCD{A}'{B}'{C}'{D}'\). Mệnh đề nào sau đây là sai?
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A\left( 1\,;\,1\,;\,0 \right)\), \(B\left( -1\,;\,0\,;\,1 \right)\), \(C\left( 1\,;\,-2\,;\,3 \right)\). Cho biết thông số của hai vectơ \(\overrightarrow{EB}=\left( -1\,;-m\,;\,1 \right)\); \(\overrightarrow{EC}=\left( 1\,;\,-2-m\,;\,3 \right)\).
Một ống phun nước có hình dạng như hình vẽ dưới. Để giữ cho ống nước được cân bằng không bị nghiêng kỹ sư sử dụng ba đoạn thép để nối các điềm C, A, G với mặt đất, các đoạn thép CD, GF, AE có độ lớn lực căng lần lượt bằng 1200N, 800N và 600 N. Trong hệ tọa độ \(Oxyz\), coi gốc tọa độ là chân ống nước, trục \(Oz\) hướng lên trời, mặt đất là mặt phẳng (\(Oxy\)) các thông số được cho như hình vẽ, đơn vị trên các hệ trục tọa độ tính bằng mét. Coi đường kính ống không đáng kể, độ lớn vectơ hợp lực của ba sợi thép tác động lên ông nước là bao nhiêu Niutơn (làm tròn kết quả đến hàng đơn vị).
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) (minh họa như hình bên).
Phát biểu nào sau đây là đúng?
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều, \(AB=1\), cạnh bên \(SE\) vuông góc với mặt phẳng đáy và \(SB=1\). Tích vô hướng của hai vectơ \(\overrightarrow{SA}\) và \(\overrightarrow{SB}\) bằng:
Xét hai chiếc khinh khí cầu bay lên từ cùng một điểm trong cùng một ngày. Lúc 9h sáng, chiếc thứ nhất đang ờ vị trí \(A\) cách điểm xuất phát 2 km về phía Nam và 1 km về phía Đông, đồng thời cách mặt đất \(0,5\text{ }\!\!~\!\!\text{ km}\). Chiếc thứ hai đang ở vị trí \(B\) nằm cách điềm xuất phát 1 km về phía Bắc và \(1,5\text{ }\!\!~\!\!\text{ km}\) về phía Tây đồng thời cách mặt đất \(0,8\text{ }\!\!~\!\!\text{ km}\). Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng (\(Oxy\)) trùng với mặt đất, trục \(Ox\) hướng về phía Nam, trục \(Oy\) hướng về phía Đông và trục Oz hướng thẳng đứng lên trời (như hình vẽ). Lấy đơn vị đo trên mỗi trục là km.
Một chiếc máy bay không người lái bay lên tại một điểm. Sau một thời gian bay, chiếc máy bay cách điểm xuất phát về phía Bắc \(50\left( km \right)\) và về phía Tây \(20\left( km \right)\), đồng thời cách mặt đất \(1\left( km \right)\). Xác định khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát của nó.
Cho hình hộp \(ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\). Véctơ\(\overrightarrow{AC}\) bằng với véctơ nào sau đây?
Cho hình lập phương \(ABCD.A'B'C'D'\) (minh họa như hình bên). Mệnh đề nào sau đây sai?
Trong hóa học, cấu tạo của phân tử amoniac \(\left( \text{N}{{\text{H}}_{3}} \right)\) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen \(\left( N \right)\) và đáy là tam giác \({{H}_{1}}{{H}_{2}}{{H}_{3}}\) với \({{H}_{1}},{{H}_{2}},{{H}_{3}}\) là vị trí của ba nguyên tử hydrogen \(\left( H \right)\). Góc tạo bởi liên kết \(H-N-H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({{H}_{1}},{{H}_{2}},{{H}_{3}}\) (chẳng hạn \({{H}_{1}}N{{H}_{2}}\)), gọi là góc liên kết của phân tử \(\text{N}{{\text{H}}_{3}}\). Góc này xấp xỉ \({{107}^{\circ }}\). Trong không gian Oxyz, cho một phân tử \(\text{N}{{\text{H}}_{3}}\) được biểu diễn bởi hình chóp tam giác đều \(N.{{H}_{1}}{{H}_{2}}{{H}_{3}}\) với \(O\) là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm \(N\) thuộc trục Oz , ba nguyên tử hydrogen ở các vị trí \({{H}_{1}},{{H}_{2}},{{H}_{3}}\) trong đó \({{H}_{1}}\left( 0;-2;0 \right)\) và \({{H}_{2}}{{H}_{3}}\) song song với trục \(Ox\) như hình vẽ minh hoạ. Khoảng cách ngắn nhất giữa các nguyên tử là bao nhiêu?
(Kết quả làm tròn đến chũ số hàng phần trăm).
Cho ba điểm\(A\left( 3;2;-1 \right)\), \(B\left( -1;4;5 \right)\), \(C\left( 1;2;-1 \right)\). Tích vô hướng \(\overrightarrow{AB}.\overrightarrow{BC}\) có giá trị là:
Cho hai vectơ \(\vec{a}\) và \(\vec{b}\) thỏa mãn \(\left| \vec{a}\left| =2,\text{ }\!\!~\!\!\text{ } \right|\vec{b} \right|=3\) và \(\vec{a}\) tạo với \(\vec{b}\) một góc bằng \({{45}^{\circ }}\). Khi đó \(\vec{a}.\vec{b}\) bằng:
