Để đo chu kì bán rã của một chất phóng xạ người ta cho máy đếm xung bắt đầu đếm từ thời điểm t = 0 đến thời điếm t₁ = 2 h máy đếm được n xung, đến thời điếm t₂ = 6 h, máy đếm được 2,3n xung. Xác định chu kì bán rã của chất phóng xạ này là bao nhiêu giờ. (Làm tròn đến hàng phần trăm)

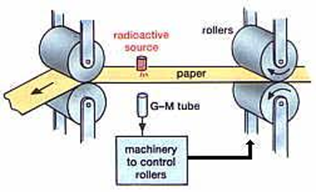
Trong một dây chuyền sản xuất giấy, người ta sử dụng khả năng đâm xuyên của tia β để kiểm tra độ dày của giấy. Cụ thể, một nguồn phóng xạ \({}_{\text{ }\!\!~\!\!\text{ }}^{85}\text{Kr}\) có chu kì bán rã 10,75 năm phát tia β được đặt ở một bên tấm giấy, phía đối diện là đầu dò ghi nhận số tia β xuyên qua. Khi giấy dày lên, ít tia β đến được đầu dò; hệ thống sẽ tự động điều chỉnh độ dày giấy về mức chuẩn. Sau một khoảng thời gian dài sử dụng, nhân viên kỹ thuật phát hiện rằng hệ thống liên tục báo tín hiệu rằng giấy bị quá dày, mặc dù độ dày giấy thực tế không thay đổi. Nguyên nhân nào sau đây là hợp lí nhất?

Tại một thời điểm, mẫu chất phóng xạ A có chu kì bán rã là 2 ngày và có 6,4.10¹¹ hạt nhân nguyên tử trong mẫu. Mẫu chất phóng xạ B có chu kì bán rã là 3 ngày và có 16.10¹⁰ hạt nhân nguyên tử trong mẫu. Sau bao nhiêu ngày nữa thì số hạt nhân nguyên tử chưa phóng xạ của hai mẫu đó bằng nhau?

Hình bên dưới biểu diễn sự thay đổi độ phóng xạ của một mẫu chất phóng xạ X theo thời gian.

Độ phóng xạ của mẫu chất \(X\) tại thời điểm 145 ngày là \(\mathrm{a} \cdot 10^{3} \mathrm{~Bq}\). Giá trị của a là bao nhiêu (làm tròn kết quả đến chữ số hàng phần mười).

Trong mỗi ý a ), b), c ), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Hình bên biểu diễn sơ đồ hoạt động của cảm biến báo khói ion hóa. Nguồn phóng xạ \(\alpha\) Americium \({ }_{95}^{241} \mathrm{Am}\) được đặt giữa hai bản kim loại nối với một pin. Các hạt \(\alpha\) được phóng ra làm ion hóa không khí giữa hai bản kim loại đặt song song và nối vào hai cực của nguồn điện, cho phép một dòng điện nhỏ chạy giữa hai bản kim loại đó và chuông báo không kêu. Nếu có khói bay vào giữa hai bản kim loại, các ion trong này sẽ kết hợp với các phân tử khói và dịch chuyển chậm hơn làm cường độ dòng điện giữa hai bản kim loại giảm đi. Khi dòng điện giảm tới mức nhất định thì cảm biến báo khói sẽ gửi tín hiệu kích hoạt đến chuông báo cháy.

Nguồn phóng xạ \(\alpha\) Americium \({ }_{95}^{241} \mathrm{Am}\) chứa trong cảm biến báo khói ion hóa có khối lượng ban đầu là \(0,2025 \mu \mathrm{~g}\).

Biết hằng số phóng xạ của \({ }_{95}^{241} \mathrm{Am}\) bằng \(5,086 \cdot 10^{-11} \mathrm{~s}^{-1}\). Lấy khối lượng nguyên tử xấp xỉ bằng số khối của nguyên tử tính theo đơn vị amu và 1 năm \(=365\) ngày.

Máy xạ trị (như hình bên) thường sử dụng nguồn phóng xạ \({ }_{27}^{60} \mathrm{Co}\) có chu kì bán rã là 5,3 năm. Để đáp ứng đúng các tiêu chí y học để điều trị bệnh, thiết bị sẽ bắt buộc phải bảo dưỡng để hiệu chỉnh lại chùm tia chiếu xạ trước khi độ phóng xạ giảm đi \(7 \%\) và phải thay nguồn phóng xạ mới trước khi độ phóng xạ giảm đi \(50 \%\). Lấy 1 năm = 12 tháng. Biết mỗi lần bảo dưỡng không làm ảnh hưởng đến nguồn phóng xạ.

Nếu thực hiện bảo dưỡng đúng lịch bảo dưỡng thì sau nhiều nhất bao nhiêu lần bảo dưỡng (với chu kì bảo dưỡng được xác định ở câu 5) thì ta cần thay nguồn phóng xạ mới?

Chất phóng xạ \({}_{6}^{14}C\) có chu kỳ bán rã là T. Ban đầu có một mẫu \({}_{6}^{14}C\) nguyên chất với khối lượng 4g. Sau khoảng thời gian 2 chu kỳ liên tiếp, khối lượng chất \({}_{6}^{14}C\) trong mẫu đã bị phân rã là

Trong thành phần sữa bò có chứa potassium với nồng độ \(2 \mathrm{~g} / \ell\). Trong đó có \(0,0117 \%\) là đồng vị phóng xạ potassium \({ }_{19}^{40} \mathrm{~K}\) với chu kì bán rã là \(1,25.10^{9}\) năm.

Sau tai nạn ở nhà máy điện hạt nhân Chernobyl vào năm 1986, người ta phát hiện có các đồng vị phóng xạ \({ }_{53}^{131}\) I trong khí quyển. Mưa sẽ làm cỏ nhiễm đồng vị phóng xạ này và cuối cùng nó xuất hiện trong sữa bò. Người ta đo được độ phóng xạ \({ }_{53}^{131} \mathrm{I}\) trong sữa bò ở Ba Lan lúc đó là \(2 \mathrm{kBq} / \ell\). Biết chu kì bán rã của \({ }_{53}^{131} \mathrm{I}\) là 8,02 ngày.

Khối lượng của nguyên tử được xem gần bằng số khối của nguyên tử tính theo đơn vị amu. Lấy một năm có 365 ngày.

Sau bao lâu thì độ phóng xạ của đồng vị phóng xạ \({ }_{53}^{131} \mathrm{I}\) có trong 3 lít sữa bò ở Ba Lan khi đó giảm xuống bằng độ phóng xạ của đồng vị phóng xạ \({ }_{19}^{40} \mathrm{~K}\) được tính ở Câu 5?

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong lĩnh vực y học, đồng vị phóng xạ \({ }_{53}^{131} \mathrm{I}\), với chu kỳ bán rã 8 ngày, được sử dụng rộng rãi trong điều trị các bệnh liên quan đến ung thư tuyến giáp. Giả sử một bệnh nhân trong liệu trình điều trị nhận được liều thuốc chứa \({ }_{53}^{131} \mathrm{I}\) với độ phóng xạ \(\mathrm{H}_{0}=2,5 \cdot 10^{15} \mathrm{~Bq}\) tại thời điểm mẫu thuốc vừa được sản xuất.

Chất phóng xạ cobalt \(_{}^{60}Co\) dùng trong y tế có chu kì bán rã 5,33 năm và khối lượng nguyên tử là 58,9 amu. Ban đầu có 500 g \(_{}^{60}Co\).

Khối lượng \(_{}^{60}Co\) còn lại sau 12 năm là

Hạt nhân \({}_{84}^{210}\text{Po}\) phóng xạ \(\text{ }\!\!\alpha\!\!\text{ }\) tạo thành hạt nhân \({}_{82}^{206}\text{Pb}\) bền. Ban đầu có một mẫu chất trong đó chứa cả hạt nhân \({}_{84}^{210}\text{Po}\) và hạt nhân \({}_{82}^{206}\text{Pb}\). Biết hạt nhân \({}_{82}^{206}\text{Pb}\) sinh ra được giữ lại hoàn toàn trong mẫu. Tại thời điểm t1, tỉ số giữa số hạt nhân \({}_{82}^{206}\text{Pb}\) và số hạt nhân \({}_{84}^{210}\text{Po}\) còn lại trong mẫu là 1. Tại thời điểm t₂ = 3,52t₁, tỉ số giữa số hạt nhân \({}_{82}^{206}\text{Pb}\) và số hạt nhân \({}_{84}^{210}\text{Po}\) còn lại trong mẫu là 7. Tỉ số giữa số hạt nhân \({}_{82}^{206}\text{Pb}\) và số hạt nhân \({}_{84}^{210}\text{Po}\) có trong mẫu chất ban đầu xấp xỉ bằng

Một mẫu chất phóng xạ \(X\) phân rã theo thời gian và phát ra các hạt \(\alpha\). Số lượng các hạt \(\alpha\) này được ghi nhận bởi một máy thu (ống Geiger - Muller) và được biểu diễn theo thời gian t như đồ thị ở hình bên dưới. Tính hằng số phóng xạ của chất phóng xạ X (làm tròn đến hàng phần trăm).

Trong một mẫu chất phóng xạ, tại thời điểm ban đầu \((\mathrm{t}=0)\), mẫu chất có \(\mathrm{N}_{0}\) hạt nhân. Biết hằng số phóng xạ và chu kì bán rã của chất phóng xạ này lần lượt là \(\lambda\) và \(T\). Sau đó một khoảng thời gian \(\Delta t\), số lượng hạt nhân còn lại trong mẫu chất đó \(\left(\mathrm{N}_{\mathrm{t}}\right)\) được xác định bằng biểu thức nào sao đây?

Đồng vị Iodine ( \({ }_{53}^{131} \mathrm{I}\) ) là chất phóng xạ \(\beta^{-}\)được sử dụng trong y học để điều trị các bệnh liên quan đến tuyến giáp. Chất này có chu kỳ bán rã là 8,04 ngày. Một bệnh nhân được chỉ định sử dụng liều Iodine131 với độ phóng xạ ban đầu là \(\mathrm{H}_{0}=5,20 \cdot 10^{8} \mathrm{~Bq}\). Coi rằng \(85 \%\) lượng Iodine \(\left({ }_{53}^{131} \mathrm{I}\right)\) trong liều đó sẽ tập trung tại tuyến giáp. Bệnh nhân được kiểm tra tuyến giáp lần thứ nhất ngay sau khi dùng liều và lần thứ hai sau 48 giờ. Biết khối lượng mol nguyên tử của Iodine là \(127 \mathrm{~g} / \mathrm{mol}\).

Trong một phòng thí nghiệm hạt nhân, các nhà khoa học sử dụng đồng vị bền \({ }_{25}^{55} \mathrm{Mn}\) để nghiên cứu sự phân rã hạt nhân. Họ tiến hành chiếu một chùm nơtron vào một mẫu mangan \({ }_{25}^{55} \mathrm{Mn}\) để tạo ra đồng vị phóng xạ \({ }_{25}^{56} \mathrm{Mn}\). Sau khi quá trình bắn phá hoàn tất, tỉ lệ giữa số nguyên tử \({ }_{25}^{56} \mathrm{Mn}\) so với \({ }_{25}^{55} \mathrm{Mn} 1 a ̀ ~ 10^{-8}\). Đồng vị \({ }_{25}^{56} \mathrm{Mn}\) có chu kỳ bán rã là 2,5 giờ và phát ra tia \(\beta^{-}\)được ứng dụng trong y học để đo lường liều phóng xạ. Sau 15 giờ kể từ khi quá trình bắn phá kết thúc, tỉ số giữa nguyên tử của hai loại hạt trên là \(\mathrm{x} \cdot 10^{-10}\). Giá trị của x là bao nhiêu? (làm tròn kết quả đến chữ số phần trăm).

Trong các biển báo dưới đây, đâu là biển báo nguy hiểm do phóng xạ?

Hiện nay, đồng vị phóng xạ \({ }_{9}^{18} \mathrm{~F}\) được sử dụng rộng rãi trong việc chẩn đoán các bệnh ung thư nhờ vào công nghệ chụp cắt lớp bằng phát xạ positron (Positron Emission Tomography - PET). Hình bên là máy PET. Giả sử rằng một bệnh nhân được tiêm một lượng chất phóng xạ \({ }_{9}^{18} \mathrm{~F}\) với độ phóng xạ là 320 Bq trước khi quá trình chụp ảnh diễn ra. Hỏi sau bao lâu kể từ thời điểm tiêm thì độ phóng xạ trong cơ thể bệnh nhân giảm còn 20 Bq ? Biết rằng chu kì bán rã của \({ }_{9}^{18} \mathrm{~F}\) là 110 ngày.

Một đồng vị phóng xạ có chu kì bán rã là 12,7 giờ. Sau 38,1 giờ, độ phóng xạ của đồng vị này giảm bao nhiêu phần trăm so với lúc ban đầu?

Chất phóng xạ chứa đồng vị \(_{11}^{24}Na\)được sử dụng làm chất đánh dấu điện giải có chu kì bán rã là 15,00 giờ. Một bệnh nhân được tiêm 5,00 ml dược chất chứa \(_{11}^{24}Na\) với nồng độ 1,002.10^-3 mol/l. Biết \({{N}_{A}}=6,{{02.10}^{23}}\)mol-1. Độ phóng xạ của liều dược chất tại thời điểm tiêm là

Phát biểu nào sau đây là sai khi nói về tia alpha \((\alpha)\) ?

Ngày 12/9/2014, một sự cố nghiêm trọng xảy ra tại TP.HCM khi Công ty TNHH Apave Châu Á – Thái Bình Dương báo cáo bị thất lạc một thiết bị chứa nguồn phóng xạ Iridium -\({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) dùng trong kiểm tra mối hàn công nghiệp. Theo hồ sơ ghi nhận vào thời điểm bàn giao thiết bị, nguồn \({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) có khối lượng ban đầu 5,0 g, được cất giữ trong một thiết bị bọc chì chuyên dụng. Chu kỳ bán rã của \({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) là khoảng 74 ngày và mỗi phân rã phát ra tia gamma mạnh. Một năm sau sự cố, các nhà chức trách tiến hành rà soát lại các thiết bị còn tồn đọng, đồng thời đo hoạt độ còn lại để xác định mức độ nguy hiểm.

Ước tính rằng 2,42.10²³ phân tử MIC tạo thành một liều lượng nguy hiểm cho con người, số lượng người tối đa có thể bị đe dọa bởi lượng MIC còn lại trong khoang chứa là bao nhiêu?