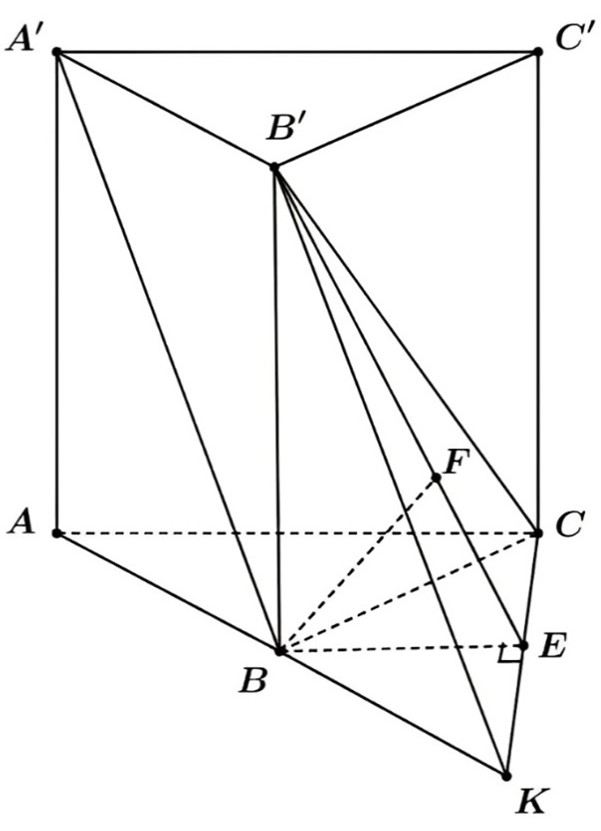
 Kẻ \(\mathrm{B}^{\prime} \mathrm{K} / / \mathrm{A}^{\prime} \mathrm{B}(\mathrm{K} \in \mathrm{AB})\).
Kẻ \(\mathrm{B}^{\prime} \mathrm{K} / / \mathrm{A}^{\prime} \mathrm{B}(\mathrm{K} \in \mathrm{AB})\).
\(\Rightarrow \mathrm{A}^{\prime} \mathrm{B} / /\left(\mathrm{B}^{\prime} \mathrm{CK}\right)\)
Suy ra \(d\left(A^{\prime} B, B^{\prime} C^{\prime}\right)=d\left(A^{\prime} B,\left(B^{\prime} C K\right)\right)=d\left(B,\left(B^{\prime} C K\right)\right)\).
Kẻ \(\mathrm{BE} \perp \mathrm{CK}(\mathrm{E} \in \mathrm{CK}) ; \mathrm{BF} \perp \mathrm{B}^{\prime} \mathrm{E}\left(\mathrm{F} \in \mathrm{B}^{\prime} \mathrm{E}\right)\).
Ta có: \(\left\{\begin{array}{l}\mathrm{BE} \perp \mathrm{CK} \mathrm{B}^{\prime} \mathrm{B} \perp \mathrm{CK} \quad\left(\mathrm{B}^{\prime} \mathrm{B} \perp(\mathrm{ABC})\right)\end{array}\right.\)
Suy ra CK \(\perp\) BF.
Ta có: \(\left\{\begin{array}{l}\mathrm{BF} \perp \mathrm{B}^{\prime} \mathrm{E} \mathrm{BF} \perp \mathrm{CK}\end{array} \Rightarrow \mathrm{BF} \perp\left(\mathrm{B}^{\prime} \mathrm{CK}\right)\right.\).
Vậy \(d\left(B,\left(B^{\prime} C K\right)\right)=B F\).
+) Trong tam giác vuông \(A^{\prime} B^{\prime} B\), ta có:
\(\mathrm{B}^{\prime} \mathrm{B}=\sqrt{\mathrm{A}^{\prime} \mathrm{B}^{2}-\mathrm{A}^{\prime} \mathrm{B}^{\prime 2}}=\sqrt{(\sqrt{6})^{2}-(\sqrt{2})^{2}}=2 .\)
+) \(\widehat{\mathrm{ABC}}=60^{\circ} \Rightarrow \widehat{\mathrm{CBK}}=180^{\circ}-60^{\circ}=120^{\circ}\).
Vì \(A^{\prime} B^{\prime} K B\) là hình bình hành nên ta có \(K B=A^{\prime} B^{\prime}=B C\).
Suy ra tam giác BCK cân tại B.
\(\Rightarrow \widehat{\mathrm{KBE}}=\frac{1}{2} \widehat{\mathrm{CBK}}=60^{\circ}\).
Xét tam giác vuông BEK , ta có \(\cos \widehat{\mathrm{KBE}}=\frac{\mathrm{BE}}{\mathrm{BK}}\).
\(\Rightarrow \mathrm{BE}=\mathrm{BK} \cdot \cos \widehat{\mathrm{KBE}}=\sqrt{2} \cdot \cos 60^{\circ}=\frac{\sqrt{2}}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(\mathrm{BB}^{\prime} \mathrm{E}\), ta có:
\(\begin{align}& \frac{1}{\mathrm{BF}^{2}}=\frac{1}{\mathrm{BB}^{\prime 2}}+\frac{1}{\mathrm{BE}^{2}} \\\Leftrightarrow & \frac{1}{\mathrm{BF}^{2}}=\frac{1}{2^{2}}+\frac{1}{\left(\frac{\sqrt{2}}{2}\right)^{2}} \\\Leftrightarrow & \frac{1}{\mathrm{BF}^{2}}=\frac{9}{4} \\\Leftrightarrow & \mathrm{BF}^{2}=\frac{4}{9} \\\Leftrightarrow & \mathrm{BF} \quad=\frac{2}{3} \approx 0,67 .\end{align}\)
 Kẻ \(\mathrm{B}^{\prime} \mathrm{K} / / \mathrm{A}^{\prime} \mathrm{B}(\mathrm{K} \in \mathrm{AB})\).
Kẻ \(\mathrm{B}^{\prime} \mathrm{K} / / \mathrm{A}^{\prime} \mathrm{B}(\mathrm{K} \in \mathrm{AB})\).














