Số phần tử của không gian mẫu: \(n\left( \text{ }\!\!\Omega\!\!\text{ } \right)=A_{9}^{6}=60480\) (cách)
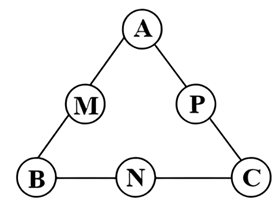
Để giải được mật thư, các số được chọn và xếp phải thỏa mãn cấp số cộng \(\left\{ \begin{array}{*{35}{l}} A+B=2M \\ B+C=2N \\ C+A=2P \\\end{array} \right.\)
Do đó tổng \(A+B;B+C;C+A\) phải là các số chẵn (Điều này xảy ra khi \(A,B,C\) phải cùng chẵn hoặc cùng lẻ)
Suy ra ta phải đi tìm bộ 6 số phân biệt \(\left\{ A,B,C,M,N,P \right\}\) trong \(S\) thỏa mãn điều kiện:
Trong tập \(S\) có \(\left\{ \begin{array}{*{35}{l}} L=\left\{ 21;23;25;27;29 \right\} \\ C=\left\{ 22;24;26;28 \right\} \\\end{array} \right.\) có 5 số chẵn và 4 số lẻ
Trường hợp 1: Ba số \(A,B,C\) đều là các số lẻ.
Ta cần chọn 3 số lẻ khác nhau từ tập \(L\) làm \(A;B;C\).
Sau đó, các số \(M,N,P\) sẽ được tính theo công thức.
Ta phải kiểm tra xem bộ 6 số tạo thành có phân biệt và đều thuộc \(S\) hay không.
Các bộ 3 số lẻ \(\left\{ A,B,C \right\}\) có thể và các bộ 6 số tương ứng \(\left\{ A,B,C,M,N,P \right\}\(:
\(\left\{ 21,23,27 \right\}\Rightarrow M=22,N=25,P=24\).
Bộ 6 số: \(\left\{ 41,43,47,42,45,44 \right\}\) (thỏa mãn)
\(\left\{ 21,23,29 \right\}\Rightarrow M=22,N=26,P=25\).
Bộ 6 số: \(\left\{ 21,23,29,22,26,25 \right\}\) (thỏa mãn)
\(\left\{ 21,25,27 \right\}\Rightarrow M=23,N=26,P=24\).
Bộ 6 số: \(\left\{ 21,25,27,23,26,44 \right\}\) (thỏa mãn)
\(\left\{ 21,27,29 \right\}\Rightarrow M=24,N=28,P=25\).
Bộ 6 số: \(\left\{ 21,27,29,24,28,25 \right\}\) (thỏa mãn)
\(\left\{ 23,25,29 \right\}\Rightarrow M=24,N=27,P=26\).
Bộ 6 số: \(\left\{ 23,25,29,24,27,26 \right\}\) (thỏa mãn)
\(\left\{ 23,27,29 \right\}\Rightarrow M=25,N=28,P=26\).
Bộ 6 số: \(\left\{ 23,27,29,25,28,26 \right\}\) (thỏa mãn)
Lưu ý: Các bộ như \(\left\{ 21,23,25 \right\}\) sẽ bị loại vì \(P=\frac{\left( 21+25 \right)}{2}=23\), trùng với \(B\).
Trường hợp 2: Ba số \(A,B,C\) đều là các số chẵn.
Ta cần chọn 3 số chẵn khác nhau từ tập \(C\) làm \(A;B;C\).
\(\left\{ 22,24,28 \right\}\Rightarrow M=23,N=26,P=45\).
Bộ 6 số: \(\left\{ 22,24,28,23,26,25 \right\}\) (thỏa mãn)
\(\left\{ 22,26,28 \right\}\Rightarrow M=24,N=27,P=25\).
Bộ 6 số: \(\left\{ 22,26,28,24,27,25 \right\}\) (thỏa mãn)
Lưu ý: Các bộ như \(\left\{ 22,24,26 \right\}\) sẽ bị loại vì \(P=\frac{\left( 22+26 \right)}{2}=24\), trùng với \(B\).
Vậy có 2 bộ số thỏa mãn trong trường hợp này nên có \(6+2=8\) bộ 6 số thỏa mãn yêu cầu.
Với mỗi bộ 6 số hợp lệ, ta đã xác định được đâu là 3 số ở các đỉnh \(\left( A;B;C \right)\) và đâu là 3 số ở các cạnh \(\left( M;N;P \right)\).
Ta có thể hoán vị 3 số ở các đỉnh \(\left( A;B;C \right)\) nên cách hoán vị là \(3!=6\) cách.
Khi 3 giá trị \(\left( A;B;C \right)\) đã được gán, các giá trị \(\left( M;N;P \right)\) sẽ được xác định duy nhất theo công thức.
Ví dụ: Với bộ \(\left\{ 21,23,27,22,25,24 \right\}\) thì nếu ta xếp \(A=21;B=23;C=27\) thì bắt buộc giá trị của ba số lần lượt là: \(M=22;N=25;P=24\).
Số cách xếp thuận lợi là: \(n\left( A \right)=8.3!=8.6=48\) (cách)
nên \(P\left( A \right)=\frac{n\left( A \right)}{n\left( \Omega \right)}=\frac{48}{60480}=\frac{1}{1260}\).
Vậy giá trị của biểu thức \(\frac{2}{a}=\frac{2}{\frac{1}{1260}}=2.1260=2520\).