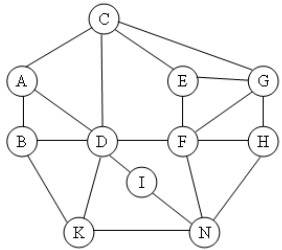
Cho đồ thị vô hướng G = (V,E), khẳng định nào sau đây là đúng?
A.
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u
B.
Thuật toán DFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị
C.
Thuật toán DFS(u) duyệt tất cả các thành phần liên thông của đồ thị
D.
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Trả lời:
Đáp án đúng: A
Phân tích câu hỏi:
Câu hỏi kiểm tra kiến thức về thuật toán tìm kiếm theo chiều sâu (DFS) trên đồ thị vô hướng.
Đánh giá các phương án:
- Phương án 1: "Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u" - Đây là khẳng định đúng. DFS bắt đầu từ một đỉnh và duyệt tất cả các đỉnh có thể đến được từ đỉnh đó, tức là duyệt thành phần liên thông chứa đỉnh đó.
- Phương án 2: "Thuật toán DFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị" - Sai, DFS chỉ tìm đường đi từ đỉnh u đến các đỉnh khác trong cùng thành phần liên thông. Nếu hai đỉnh không thuộc cùng một thành phần liên thông, DFS sẽ không tìm thấy đường đi giữa chúng.
- Phương án 3: "Thuật toán DFS(u) duyệt tất cả các thành phần liên thông của đồ thị" - Sai, DFS(u) chỉ duyệt thành phần liên thông chứa đỉnh u. Để duyệt tất cả các thành phần liên thông của đồ thị, cần phải gọi DFS cho mỗi đỉnh chưa được thăm trong đồ thị.
- Phương án 4: "Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần" - Sai, DFS(u) chỉ duyệt các đỉnh trong thành phần liên thông của u một lần. Nếu đồ thị không liên thông, nó sẽ không duyệt hết tất cả các đỉnh của đồ thị.
Kết luận:
Phương án 1 là khẳng định đúng nhất.
Bộ 525 câu hỏi trắc nghiệm ôn thi môn Toán rời rạc có đáp án dưới đây sẽ là tài liệu ôn tập hữi ích dành cho các bạn sinh viên. Mời các bạn cùng tham khảo!
30 câu hỏi 60 phút