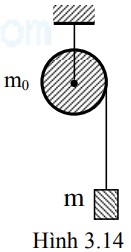
Khối cầu đặc đồng chất, tâm O, bán kính R, khối lượng m phân bố đều. Người ta khoét bên trong khối cầu đó một lỗ hổng cũng có dạng hình cầu tâm O’, bán kính r = R/2. Nếu O’ cách O một đoạn d = R/2 thì mômen quán tính của phần còn lại của khối cầu đối với trục quay chứa O và O’ là:

\(I = \frac{2}{5}m{R^2}\)

\(I = \frac{3}{2}m{R^2}\)

\(I = \frac{31}{70}m{R^2}\)

\(I = \frac{31}{80}m{R^2}\)

Trả lời:

Đáp án đúng: D

Gọi khối lượng của khối cầu lớn là m, thì khối lượng của phần bị khoét là m'. Vì khối lượng phân bố đều nên: \(\frac{m'}{m} = \frac{V'}{V} = \frac{\frac{4}{3}\pi r^3}{\frac{4}{3}\pi R^3} = \frac{r^3}{R^3} = \frac{(\frac{R}{2})^3}{R^3} = \frac{1}{8}\) => \(m' = \frac{m}{8}\) Mômen quán tính của khối cầu lớn đối với trục OO' là: \(I = \frac{2}{5}mR^2\) Mômen quán tính của phần bị khoét đối với trục OO' là: \(I' = I_{CM} + m'd^2 = \frac{2}{5}m'r^2 + m'd^2 = \frac{2}{5}.\frac{m}{8}.(\frac{R}{2})^2 + \frac{m}{8}.(\frac{R}{2})^2 = \frac{mR^2}{80} + \frac{mR^2}{32} = \frac{7mR^2}{160}\) Mômen quán tính của phần còn lại là: \(I_{cl} = I - I' = \frac{2}{5}mR^2 - \frac{7mR^2}{160} = \frac{64mR^2 - 7mR^2}{160} = \frac{57mR^2}{160} = \frac{31}{80}mR^2\)

520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Phần 1

500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 35:

Một đĩa tròn mỏng đồng chất, khối lượng phân bố đều, bán kính R, bị khoét một lỗ hình tròn, bán kính r = R/2. Tâm O’ của lỗ thủng cách tâm O của đĩa một khoảng R/2. Khối lượng của phần còn lại là m. Mômen quán tính của phần còn lại đối với trục quay đi qua O và O’là:

Lời giải:

Đáp án đúng: D

Gọi \(\rho\) là mật độ khối lượng trên đơn vị diện tích của đĩa. Khối lượng của đĩa ban đầu là \(M = \rho \pi R^2\). Khối lượng của phần bị khoét là \(m' = \rho \pi r^2 = \rho \pi (R/2)^2 = M/4\). Do đó, khối lượng của phần còn lại là \(m = M - M/4 = 3M/4\), suy ra \(M = 4m/3\). Mômen quán tính của đĩa tròn ban đầu đối với trục quay đi qua tâm O là \(I = \frac{1}{2}MR^2 = \frac{1}{2} \cdot \frac{4m}{3} R^2 = \frac{2}{3}mR^2\). Mômen quán tính của phần bị khoét đối với trục quay đi qua tâm O' là \(I' = \frac{1}{2}m'r^2 = \frac{1}{2} \cdot \frac{M}{4} \cdot (R/2)^2 = \frac{1}{32}MR^2 = \frac{1}{32} \cdot \frac{4m}{3} R^2 = \frac{1}{24}mR^2\). Áp dụng định lý Steiner, mômen quán tính của phần bị khoét đối với trục quay đi qua O là \(I_O' = I' + m'(OO')^2 = \frac{1}{24}mR^2 + \frac{M}{4} \cdot (R/2)^2 = \frac{1}{24}mR^2 + \frac{1}{4} \cdot \frac{4m}{3} \cdot \frac{R^2}{4} = \frac{1}{24}mR^2 + \frac{1}{12}mR^2 = \frac{1}{8}mR^2\). Mômen quán tính của phần còn lại đối với trục quay đi qua O là \(I_{cl} = I - I_O' = \frac{2}{3}mR^2 - \frac{1}{8}mR^2 = \frac{16 - 3}{24}mR^2 = \frac{13}{24}mR^2\).

Câu 36:

Một dây mảnh, nhẹ, không co giãn, quấn quanh một trụ đặc đồng chất khối lượng m₀ = 2kg. Đầu kia của dây nối với vật m = 1kg (hình 3.14). Bỏ qua ma sát ở trục quay, lấy g = 10m/s². Tính gia tốc của vật.

Lời giải:

Đáp án đúng: B

Gọi T là lực căng dây, a là gia tốc của vật m. Áp dụng định luật II Newton cho vật m: m*g - T = m*a (1) Áp dụng phương trình mômen lực cho trụ: T*R = I*γ = (1/2)*m0*R^2 * (a/R) => T = (1/2)*m0*a (2) Thay (2) vào (1): m*g - (1/2)*m0*a = m*a => a = m*g / (m + (1/2)*m0) = 1*10 / (1 + (1/2)*2) = 5 m/s^2

Câu 37:

Một dây mảnh, nhẹ, không co giãn, quấn quanh một trụ đặc đồng chất khối lượng m₀ = 2kg. Đầu kia của dây nối với vật m = 1kg (hình 3.14). Bỏ qua ma sát ở trục quay, lấy g = 10m/s². Tính lực căng dây nối vật m.

Lời giải:

Đáp án đúng: B

Gọi T là lực căng dây, a là gia tốc của vật m, và α là gia tốc góc của trụ. Áp dụng định luật II Newton cho vật m: m.g - T = m.a Áp dụng phương trình mô men lực cho trụ: T.R = I.α, với I là mô men quán tính của trụ đối với trục quay và R là bán kính của trụ. Vì dây không trượt trên trụ, ta có a = α.R Mô men quán tính của trụ đặc đồng chất là I = (1/2)m₀.R² Thay các phương trình trên vào, ta có: T.R = (1/2)m₀.R². (a/R) => T = (1/2)m₀.a Từ phương trình m.g - T = m.a, ta có T = m.g - m.a Thay T = (1/2)m₀.a vào, ta có m.g - (1/2)m₀.a = m.a => m.g = m.a + (1/2)m₀.a = a(m + (1/2)m₀) => a = m.g / (m + (1/2)m₀) = 1*10 / (1 + (1/2)*2) = 10 / 2 = 5 m/s² => T = (1/2)m₀.a = (1/2)*2*5 = 5 N Vậy lực căng dây là 5N.

Câu 38:

Một vô lăng đang quay với vận tốc góc ωo thì bị hãm dừng lại bởi một lực có mômen hãm tỉ lệ với căn bậc hai của vận tốc góc của vô lăng. Vận tốc góc trung bình của vô lăng trong thời gian hãm là:

Lời giải:

Đáp án đúng: B

Gọi M là mô men hãm, ta có M = -k√ω, với k > 0. Áp dụng phương trình động lực học cho chuyển động quay: Iγ = M, suy ra I(dω/dt) = -k√ω. Từ đó, dω/√ω = -(k/I)dt. Lấy tích phân hai vế từ thời điểm ban đầu (ω = ω₀, t = 0) đến thời điểm t bất kỳ, ta được: ∫(ω₀→ω) dω/√ω = ∫(0→t) -(k/I)dt => 2√ω |(ω₀→ω) = -(k/I)t |(0→t) => 2(√ω - √ω₀) = -(k/I)t => √ω = √ω₀ - (k/2I)t Khi vô lăng dừng hẳn (ω = 0), ta có thời gian hãm là t_h = (2I√ω₀)/k. Vận tốc góc tức thời là ω = (√ω₀ - (k/2I)t)² Vận tốc góc trung bình được tính bằng: ω_tb = (1/t_h) ∫(0→t_h) ω dt = (1/t_h) ∫(0→t_h) (√ω₀ - (k/2I)t)² dt Đặt x = √ω₀ - (k/2I)t, suy ra dx = -(k/2I)dt => dt = -(2I/k)dx Khi t = 0, x = √ω₀; khi t = t_h, x = 0. Do đó, ω_tb = (1/t_h) ∫(√ω₀→0) x² (-2I/k) dx = (2I/kt_h) ∫(0→√ω₀) x² dx = (2I/kt_h) [x³/3] |(0→√ω₀) = (2I/kt_h) (ω₀√ω₀/3) Thay t_h = (2I√ω₀)/k vào, ta được: ω_tb = (2I/k) * (k/(2I√ω₀)) * (ω₀√ω₀/3) = ω₀/3

Câu 39:

Một chi tiết máy gồm hai vô lăng hình trụ đặc, đồng chất, khối lượng và bán kính lần lượt là m₁, R₁ và m₂, R₂, gắn đồng trục (hình 3.20). Biết khối lượng của các vật A, B là mA = 3kg, mB = 5kg và R₁ = 2R₂. Vật A sẽ:

Lời giải:

Đáp án đúng: B

Để xác định vật A đi lên, đi xuống hay đứng yên, ta cần so sánh moment lực tác dụng lên hệ từ hai vật A và B. Moment quán tính của vô lăng 1 là I1 = (1/2)m1R1^2 và của vô lăng 2 là I2 = (1/2)m2R2^2. Vì R1 = 2R2, ta đặt R2 = R thì R1 = 2R. Ta có tỉ số R1/R2 = 2/1. Gọi a là gia tốc của vật A và vật B. Ta có a = α1*R1 = α2*R2, với α1 và α2 là gia tốc góc của vô lăng 1 và 2. Moment lực do vật A tạo ra là M_A = m_A*g*R_1. Moment lực do vật B tạo ra là M_B = m_B*g*R_2. Ta so sánh hai moment lực này. M_A = 3*g*2R = 6gR M_B = 5*g*R = 5gR Vì M_A > M_B nên vật A có xu hướng kéo hệ quay theo chiều làm cho nó đi xuống, tức là vật A đi xuống.

Câu 40:

Một ôtô chuyển động từ A, qua các điểm B, C rồi đến D. Đoạn AB dài 50km, đường khó đi nên xe chạy với tốc độ 20km/h. Đoạn BC xe chạy với tốc độ 80 km/h, sau 3h30’ thì tới C. Tại C xe nghỉ 50 phút rồi đi tiếp đến D với vận tốc 30km/h. Tính tốc độ trung bình trên toàn bộ quãng đường từ A đến D, biết CD = 3AB.

Lời giải: