Câu hỏi:
Tìm hệ số của \(x^{4}\) trong khai triển \(P(x)=\left(1-x-3 x^{3}\right)^{n}\) với \(n\) là số tự nhiên thỏa mãn hệ thức \(C_{n}^{n-2}+6 n+5=A_{n+1}^{2}\).
Đáp án đúng: C
Từ phương trình \(C_{n}^{n-2}+6 n+5=A_{n+1}^{2} \rightarrow n=10\).
Với \(n=10\), khi đó \(P(x)=\left(1-x-3 x^{3}\right)^{n}=\left(1-x-3 x^{3}\right)^{10}\).
Theo khai triển nhị thức Newton, ta có
\(P(x)=\left(1-x-3 x^{3}\right)^{10}=\left[1-\left(x+3 x^{3}\right)\right]^{10}=\sum_{k=0}^{10} C_{10}^{k}(-1)^{k}\left(x+3 x^{3}\right)^{k}\)
\(=\sum_{k=0}^{10} C_{10}^{k}(-1)^{k} x^{k}\left(1+3 x^{2}\right)^{k}=\sum_{k=0}^{10} C_{10}^{k} \sum_{l=0}^{k} C_{k}^{l}(-1)^{k} 3^{l} x^{k+2 l}\).
Số hạng chứa \(x^{4}\) trong khai triển tương ứng với \(\left\{\begin{array}{l}k+2 l=4 \\ 0 \leq k \leq 10 \\ 0 \leq l \leq k\end{array} \Leftrightarrow(k ; l)=\{(4 ; 0),(2 ; 1)\}\right.\).
Vậy hệ số của số hạng chứa \(x^{4}\) trong khai triển là \(C_{10}^{4} C_{4}^{0}+C_{10}^{2} C_{2}^{1} 3=480\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

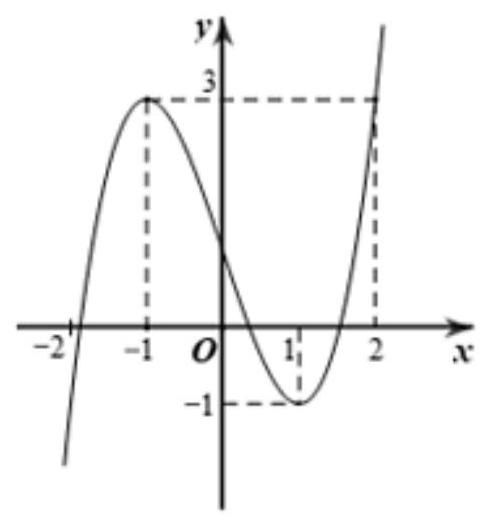 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)