Câu hỏi:
Cho phản ứng hạt nhân \({}_{3}^{6}\text{Li}+{}_{1}^{2}\text{D}\to \text{ }\!\!~\!\!\text{ }{}_{2}^{4}\text{He}+{}_{2}^{4}\text{He}\). Khối lượng của các hạt \({}_{3}^{6}\text{Li}\), \({}_{1}^{2}\text{D}\) và \({}_{2}^{4}\text{He}\) lần lượt là 6,0135 amu, 2,0136 amu và 4,0015 amu. Lấy \(1\text{u}=931,5\) MeV/c2. Phản ứng hạt nhân này
Đáp án đúng: B
Năng lượng của phản ứng hạt nhân:
\(E=\left( {{m}_{trc}}-{{m}_{sau}} \right){{c}^{2}}=\left( {{m}_{Li}}+{{m}_{D}}-2.{{m}_{He}} \right){{c}^{2}}=\left( 6,0135+2,0136-2.4,0015 \right).931,5~MeV\)
\(E\approx 22,4\) MeV > 0.
Vậy phản ứng hạt nhân này tỏa ra 22,4 MeV.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Năm 2025 - Vật Lí - Bộ Đề 07 là tài liệu ôn tập quan trọng dành cho học sinh lớp 12, giúp các em rèn luyện kỹ năng làm bài và chuẩn bị tốt nhất cho kỳ thi tốt nghiệp THPT 2025. Bộ đề được biên soạn theo định hướng của Bộ GD ĐT, bám sát chương trình học, bao gồm các chủ đề quan trọng như cơ học, điện học, quang học, dao động và sóng, vật lý hạt nhân… Hệ thống câu hỏi trắc nghiệm phong phú, được thiết kế theo nhiều mức độ từ nhận biết, thông hiểu đến vận dụng và vận dụng cao, giúp học sinh làm quen với cấu trúc đề thi và phát triển kỹ năng phân tích, tư duy logic. Mỗi đề thi đều có đáp án chi tiết và hướng dẫn giải cụ thể, hỗ trợ học sinh tự đánh giá năng lực, xác định điểm mạnh và cải thiện điểm yếu trong quá trình ôn tập.
Câu hỏi liên quan
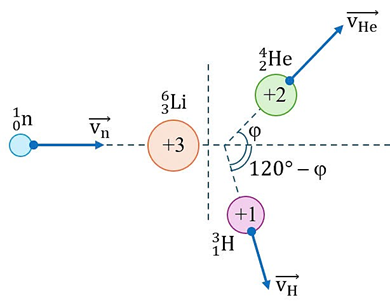
Áp dụng định luật bảo toàn động lượng, ta có:
\(\overrightarrow{{{p}_{n}}}=\overrightarrow{{{p}_{He}}}+\overrightarrow{{{p}_{H}}}\) (\({{p}_{Li}}=0\))
Ta có hình vẽ sau:
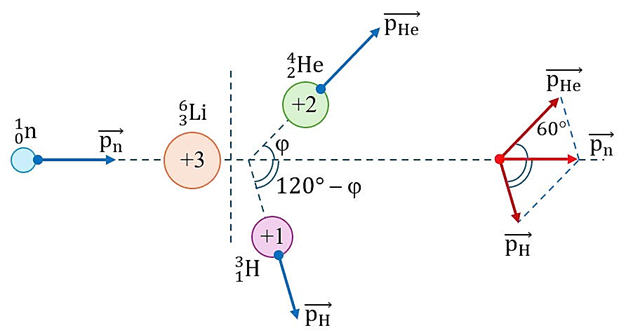
Áp dụng định lí sin, ta có:
\(\dfrac{{{p}_{He}}}{\sin \left( 120{}^\circ -\varphi \right)}=\dfrac{{{p}_{H}}}{\sin \varphi }=\dfrac{{{p}_{n}}}{\sin 60{}^\circ }\) \(\dfrac{p_{He}^{2}}{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}=\dfrac{p_{H}^{2}}{si{{n}^{2}}\varphi }=\dfrac{p_{n}^{2}}{si{{n}^{2}}60{}^\circ }\)
Mà: \({{p}^{2}}=2mK\)
Suy ra: \(\dfrac{2{{m}_{He}}.{{K}_{He}}}{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}=\dfrac{2{{m}_{H}}.{{K}_{H}}}{si{{n}^{2}}\varphi }=\dfrac{2{{m}_{n}}.{{K}_{n}}}{si{{n}^{2}}60{}^\circ }\) \(\dfrac{4.{{K}_{He}}}{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}=\dfrac{3.{{K}_{H}}}{si{{n}^{2}}\varphi }=\dfrac{1.{{K}_{n}}}{0,75}\)
Suy ra: \({{K}_{He}}=\dfrac{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}{3}.{{K}_{n}}\); \({{K}_{H}}=\dfrac{si{{n}^{2}}\varphi }{2,25}.{{K}_{n}}\) (1)
Áp dụng định luật bảo toàn năng lượng toàn phần, ta có:
\({{m}_{n}}{{c}^{2}}+{{K}_{n}}+{{m}_{Li}}{{c}^{2}}+{{K}_{Li}}={{m}_{He}}{{c}^{2}}+{{K}_{He}}+{{m}_{H}}{{c}^{2}}+{{K}_{H}}\)
\({{K}_{n}}-{{K}_{He}}-{{K}_{H}}+\left( {{m}_{n}}+{{m}_{Li}}-{{m}_{He}}-{{m}_{H}} \right){{c}^{2}}=0\)
\({{K}_{n}}-{{K}_{He}}-{{K}_{H}}+E=0\) (2)
Từ (1) và (2), suy ra: \({{K}_{n}}-\dfrac{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}{3}.{{K}_{n}}-\dfrac{si{{n}^{2}}\varphi }{2,25}.{{K}_{n}}-1,87=0\)
\({{K}_{n}}=\dfrac{1,87}{1-\dfrac{si{{n}^{2}}\left( 120{}^\circ -\varphi \right)}{3}-\dfrac{si{{n}^{2}}\varphi }{2,25}}\)
Sử dụng tính năng Table trên máy tính cầm tay, ta xác định được \({{K}_{{{n}_{\left( max \right)}}}}\approx 4,552\) MeV khi \(\varphi \approx 67{}^\circ \).
Một học sinh thực hiện thí nghiệm xác định nhiệt dung riêng của thanh đồng bằng phương pháp cân bằng nhiệt. Các dữ kiện được xác định sau:
· Thanh đồng có khối lượng \({{\text{m}}_{1}}=150\) g, được nung nóng đến nhiệt độ \({{\text{t}}_{1}}=100\) °C.
· Nước trong nhiệt lượng kế có khối lượng \({{\text{m}}_{2}}=250\) g và nhiệt độ ban đầu \({{\text{t}}_{2}}=25\) °C.
Sau khi thả thanh đồng vào nước, học sinh ghim nhiệt kế vào nước và quan sát. Khi giá trị của nhiệt kế không thay đổi nữa và hiển thị 28 °C.
Cho nhiệt dung riêng của nước là \({{\text{c}}_{\text{n}\text{c}}}=4200\) J/(kg.K). Bỏ qua sự trao đổi nhiệt với nhiệt lượng kế và môi trường bên ngoài. Gọi \({{\text{c}}_{\text{}\text{ng}}}\) (J/(kg.K)) và \({{\text{t}}_{\text{cb}}}\) (°C) lần lượt là nhiệt dung riêng của đồng và nhiệt độ của hệ khi xảy ra cân bằng nhiệt
Nhiệt lượng do thanh đồng tỏa ra bằng nhiệt lượng nước thu vào
Công thức dùng để tính nhiệt dung riêng của đồng là \({{\text{c}}_{\text{}\text{ng}}}=\dfrac{{{\text{m}}_{2}}.{{\text{c}}_{\text{n}\text{c}}}.\left( {{\text{t}}_{\text{cb}}}-{{\text{t}}_{2}} \right)}{{{\text{m}}_{1}}.\left( {{\text{t}}_{1}}-{{\text{t}}_{\text{cb}}} \right)}\)
Giá trị nhiệt dung riêng của đồng thu được trong thí nghiệm xấp xỉ bằng 233 J/(kg.K)
Nếu tính đến sự trao đổi nhiệt với nhiệt lượng kế và môi trường thì giá trị nhiệt dung riêng tính được của đồng sẽ nhỏ hơn so với giá trị thực tế
a) ĐÚNG
Do bỏ qua sự trao đổi nhiệt với nhiệt lượng kế và môi trường bên ngoài nên chỉ có sự trao đổi nhiệt giữa thanh đồng và nước (hệ cô lập về nhiệt).
Vậy nhiệt lượng do thanh đồng tỏa ra bằng nhiệt lượng nước thu vào.
b) ĐÚNG
Áp dụng phương trình cân bằng nhiệt, ta có:
\(\left| {{Q}_{ta}} \right|=\left| {{Q}_{thu}} \right|\) \({{m}_{1}}.{{c}_{ng}}.\left( {{t}_{1}}-{{t}_{cb}} \right)={{m}_{2}}.{{c}_{nc}}.\left( {{t}_{cb}}-{{t}_{2}} \right)\)
\({{c}_{ng}}=\dfrac{{{m}_{2}}.{{c}_{nc}}.\left( {{t}_{cb}}-{{t}_{2}} \right)}{{{m}_{1}}.\left( {{t}_{1}}-{{t}_{cb}} \right)}\)
c) SAI
Giá trị nhiệt dung riêng của đồng thu được trong thí nghiệm:
\({{c}_{ng}}=\dfrac{{{m}_{2}}.{{c}_{nc}}.\left( {{t}_{cb}}-{{t}_{2}} \right)}{{{m}_{1}}.\left( {{t}_{1}}-{{t}_{cb}} \right)}=\dfrac{0,25.4200.\left( 28-25 \right)}{0,15.\left( 100-28 \right)}\approx 292\) J/(kg.K).
d) ĐÚNG
Trong thực tế có tổn thất nhiệt, một phần nhiệt từ thanh đồng thoát ra môi trường nên lượng nhiệt còn lại truyền cho nước sẽ ít hơn, nước sẽ tăng nhiệt độ ít hơn. Vì vậy, nhiệt độ cân bằng thực tế sẽ thấp hơn so với trường hợp lý tưởng.
Mà: \({{c}_{ng}}=\dfrac{{{m}_{2}}.{{c}_{nc}}.\left( {{t}_{cb}}-{{t}_{2}} \right)}{{{m}_{1}}.\left( {{t}_{1}}-{{t}_{cb}} \right)}\)
Suy ra, hiệu \(\left( {{t}_{cb}}-{{t}_{2}} \right)\) giảm làm giá trị \({{c}_{ng}}\) giảm; hiệu \(\left( {{t}_{1}}-{{t}_{cb}} \right)\) tăng làm giá trị \({{c}_{ng}}\) giảm.
Vậy nếu tính đến sự trao đổi nhiệt với nhiệt lượng kế và môi trường thì giá trị nhiệt dung riêng tính được của đồng sẽ nhỏ hơn so với giá trị thực tế.
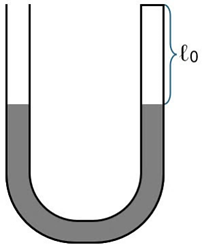
Một xi lanh thẳng đứng có một đầu kín và một đầu hở, bên trong có chứa một lượng khí hydrogen (xem là khí lí tưởng). Xi lanh được đậy kín nhờ một pit tông nhẹ, phía trên pit tông có một cột chất lỏng như hình vẽ bên. Lượng khí hydrogen luôn được cung cấp nhiệt chậm để giãn nở đẩy pit tông di chuyển từ từ. Khi toàn bộ chất lỏng bị tràn ra ngoài thì nhiệt lượng mà lượng khí hydrogen đã nhận được là 119 J. Biết rằng, thể tích ban đầu của chất lỏng bằng một nửa thể tích của lượng khí hydrogen và bằng thể tích của phần không khí chiếm trong xi lanh. Áp suất của cột chất lỏng là \(\dfrac{1}{9}{{\text{p}}_{0}}\) với \({{\text{p}}_{0}}={{10}^{5}}\) Pa là áp suất khí quyển. Bỏ qua mọi ma sát. Biết nội năng của n mol khí hydrogen ở nhiệt độ T (K) là \(\text{U}=\dfrac{5}{2}\text{nRT}\). Độ lớn công mà khối khí lí tưởng thực hiện để biến đổi từ trạng thái A sang trạng thái B bằng diện tích hình phẳng giới hạn bởi đồ thị biểu diễn sự biến đổi của áp suất theo thể tích \(\text{p}=\text{p}\left( \text{V} \right)\), trục hoành và hai đường thẳng \(\text{V}={{\text{V}}_{\text{A}}}\) và \(\text{V}={{\text{V}}_{\text{B}}}\).
Trong quá trình pit tông bắt đầu di chuyển đến khi chất lỏng bắt đầu tràn ra ngoài, áp suất của lượng khí hydrogen không đổi. Sau đó, áp suất của lượng khí hydrogen giảm dần cho đến khi toàn bộ lượng chất lỏng bị tràn ra ngoài
Thể tích ban đầu của lượng khí hydrogen là 0,36 lít
Công mà lượng khí hydrogen đã thực hiện cho đến khi toàn bộ chất lỏng bị tràn ra ngoài có độ lớn bằng 19,5 J
a) ĐÚNG
Trong quá trình pit tông bắt đầu di chuyển đến khi chất lỏng bắt đầu tràn ra ngoài, lượng khí hydrogen được cung cấp nhiệt chậm để pit tông di chuyển từ từ nên áp suất của lượng khí hydrogen không đổi. Sau đó, chất lỏng bắt đầu tràn ra ngoài làm cho áp suất tác dụng lên lượng khí giảm dần. Mà pit tông vẫn di chuyển từ từ nên áp suất của lượng khí hydrogen cũng giảm dần cho đến khi toàn bộ lượng chất lỏng bị tràn ra ngoài.
b) ĐÚNG
Xét quá trình từ khi bắt đầu cung cấp nhiệt đến khi toàn bộ chất lỏng bị tràn ra ngoài:

+ Các trạng thái của lượng khí hydrogen:
+ Quá trình biến đổi trạng thái của lượng khí hydrogen được biểu diễn trên hệ toạ độ (p,V) như sau:
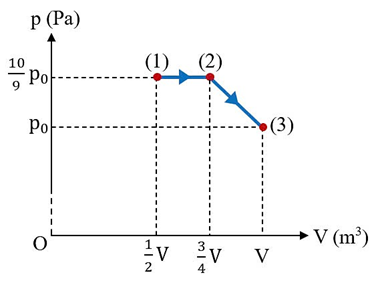
+ Độ biến thiên nội năng của lượng khí hydrogen:
\(U=\dfrac{5}{2}nR\left( {{T}_{3}}-{{T}_{1}} \right)=A+Q\)
\(\dfrac{5}{2}\left( {{p}_{3}}{{V}_{3}}-{{p}_{1}}{{V}_{1}} \right)=-\left[ \dfrac{10}{9}{{p}_{0}}\left( \dfrac{3}{4}V-\dfrac{1}{2}V \right)+\dfrac{1}{2}\left( \dfrac{10}{9}{{p}_{0}}+{{p}_{0}} \right)\left( V-\dfrac{3}{4}V \right) \right]+119\)
\(\dfrac{5}{2}\left( {{p}_{0}}V-\dfrac{10}{9}{{p}_{0}}.\dfrac{1}{2}V \right)=-\dfrac{13}{24}{{p}_{0}}V+119\)
\(\dfrac{10}{9}{{p}_{0}}V=-\dfrac{13}{24}{{p}_{0}}V+119\)
\(\dfrac{119}{72}{{p}_{0}}V=119\)
\(V=0,00072~{{m}^{3}}=0,72\) ℓ
Vậy thể tích ban đầu của lượng khí hydrogen là \(\dfrac{1}{2}V=\dfrac{1}{2}.0,72=0,36\) ℓ.
c) SAI
Công mà lượng khí hydrogen đã thực hiện cho đến khi toàn bộ chất lỏng bị tràn ra ngoài có độ lớn bằng:
\(A=\dfrac{13}{24}{{p}_{0}}V=\dfrac{13}{24}{{.10}^{5}}.0,00072=39\) J.
d) SAI
Từ khi bắt đầu cung cấp nhiệt đến khi toàn bộ chất lỏng bị tràn ra ngoài thì độ biến thiên nội năng của lượng khí hydrogen là: \(U=A+Q=-39+119=80\) J.
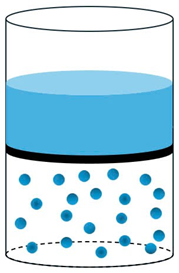
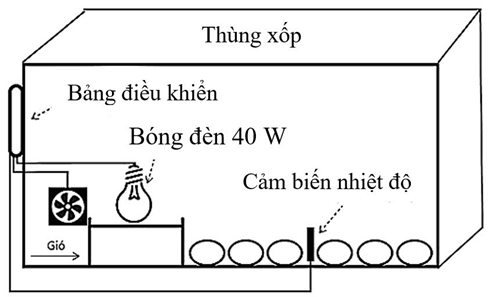
Người ta chế tạo một máy ấp trứng gà bằng thùng xốp kín được bọc cách nhiệt, có một lỗ nhỏ gắn quạt. Bên trong thùng có một bóng đèn sợi đốt, dùng để cung cấp nhiệt cho khối khí trong thùng (xem là khí lí tưởng). Khi đèn sáng, quạt cũng được bật để giúp nhiệt độ trong thùng được tăng đều (khi đó có thể xem thùng là kín, không trao đổi chất với bên ngoài).
Biết nhiệt độ và khối khí khi đèn bắt đầu mở là 27 °C và 140 g. Khi đạt đến nhiệt độ yêu cầu, cảm biến nhiệt sẽ truyền tín hiệu cho bảng điều khiển để tắt đèn và quạt. Bỏ qua sự hấp thụ nhiệt của bóng đèn và thùng xốp. Biết nhiệt dung riêng của không khí là 1005 J/(kg.K).
Trên bóng đèn sợi đốt có ghi 220 V – 40 W. Biết điện áp giữa hai đầu bóng đèn này có đồ thị biểu diễn sự biến thiên của điện áp theo thời gian u(t) như hình vẽ bên dưới.
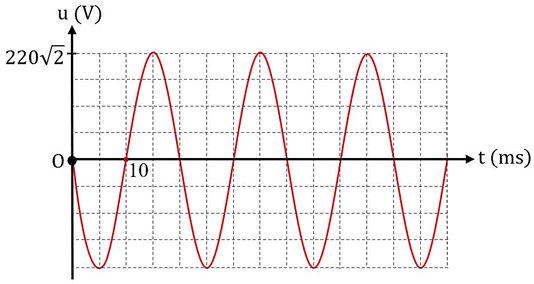
Tần số của dòng điện chạy qua bóng đèn là 50 Hz
Biểu thức cường độ dòng điện tức thời chạy qua bóng đèn là \(\text{i}=2\sqrt{2}\cos \left( 100\text{ }\!\!\pi\!\!\text{ t}+\dfrac{\pi }{2} \right)\) (A)
Để nhiệt độ khối khí trong thùng xốp đạt 37 °C (khi thùng trống) thì thời gian đèn sợi đốt phát sáng xấp xỉ bằng 35 s
a) ĐÚNG
Dựa vào đồ thị ta xác định được chu kì của điện áp là: \(T={{2.10.10}^{-3}}=0,02\) s.
Tần số của dòng điện là: \(f=\dfrac{1}{T}=\dfrac{1}{0,02}=50\) Hz.
b) SAI
Điện trở của bóng đèn: \(R=\dfrac{{{U}^{2}}}{\mathcal{P}}=\dfrac{{{220}^{2}}}{40}=1210\) W.
Pha ban đầu của điện áp: Tại \(t=0\), \(\cos {{\varphi }_{u}}=\dfrac{u\left( 0 \right)}{{{U}_{0}}}=0\) Û \({{\varphi }_{u}}=\pm \dfrac{\pi }{2}\) (rad).
Mà \(u\left( t \right)\) đang giảm nên \({{\varphi }_{u}}=\dfrac{\pi }{2}\) (rad).
Biểu thức cường độ dòng điện tức thời chạy qua bóng đèn:
\(i=\dfrac{{{U}_{0}}}{R}\cos \left( 2\pi ft+{{\varphi }_{u}} \right)\) (do mạch điện chỉ có đèn nên u(t) và i(t) cùng pha)
\(i=\dfrac{220\sqrt{2}}{1210}\cos \left( 2\pi .50t+\dfrac{\pi }{2} \right)=\dfrac{2\sqrt{2}}{11}\cos \left( 100\pi t+\dfrac{\pi }{2} \right)\) (A).
c) SAI
Nhiệt lượng do dây tóc bóng đèn tỏa ra trong mỗi giây:
\(Q=\mathcal{P}.t=40.1=40\) J (Do \(U={{U}_{M}}\) nên đèn hoạt động đúng công suất định mức).
d) ĐÚNG
Khi trong thùng trống và bỏ qua sự hấp thụ nhiệt của bóng đèn và thùng xốp, nhiệt lượng do bóng đèn tỏa ra bằng nhiệt lượng khối khí thu vào để tăng nhiệt độ. Ta có:
\({{Q}_{ta}}={{Q}_{thu}}\) \(\mathcal{P}t=mcT\) (đèn hoạt động đúng công suất định mức)
\(t=\dfrac{mcT}{\mathcal{P}}=\dfrac{0,14.1005.\left( 37-27 \right)}{40}\approx 35\) s.
Để nhiệt độ khối khí trong thùng xốp đạt 37 °C (khi thùng trống) thì thời gian đèn sợi đốt phát sáng xấp xỉ bằng 35 s.
Cho phản ứng hạt nhân \({}_{1}^{3}\text{T}+{}_{1}^{2}\text{D}\to {}_{2}^{4}\text{He}+{}_{0}^{1}\text{n}\). Khối lượng của các hạt nhân \({}_{1}^{3}\text{T}\); \({}_{1}^{2}\text{D}\); \({}_{2}^{4}\text{He}\) và hạt neutron lần lượt là \({{\text{m}}_{\text{T}}}=3,01605\text{u}\); \({{\text{m}}_{\text{D}}}=2,0141104\text{u}\); \({{\text{m}}_{\text{He}}}=4,0026\text{u}\) và \({{\text{m}}_{\text{n}}}=1,00867\text{u}\). Lấy \(1\text{u}{{\text{c}}^{2}}=931,5\) MeV; \(1\text{eV}=1,{{6.10}^{-19}}\) J. Biết năng suất tỏa nhiệt của than đá là \(\text{q}=1,{{25.10}^{7}}\) J/kg
Năng lượng tỏa ra của phản ứng hạt nhân trên xấp xỉ bằng 17,6 MeV
Năng lượng tỏa ra khi đốt cháy hoàn toàn 1 kg than đá là \(1,{{25.10}^{4}}\) J
Cần đốt cháy hoàn toàn \(2,{{112.10}^{14}}\) tấn than đá để có năng lượng tỏa ra tương đương năng lượng tỏa ra của phản ứng hạt nhân trên khi tổng hợp được 1g He
a) ĐÚNG
Năng lượng tỏa ra của phản ứng trên là:
\(E=\left( {{m}_{trc}}-{{m}_{sau}} \right){{c}^{2}}=\left( {{m}_{T}}+{{m}_{D}}-{{m}_{He}}-{{m}_{n}} \right){{c}^{2}}\)
\(E=\left( 3,01605+2,0141104-4,0026-1,00867 \right).931,5\) MeV
\(E\approx 17,6\) MeV.
b) ĐÚNG
Số nguyên tử có trong 1 g khí helium là:
\(N=\dfrac{m}{M}.{{N}_{A}}=\dfrac{1}{4}.6,{{02.10}^{23}}\approx 1,{{5.10}^{23}}\) nguyên tử.
c) SAI
Năng lượng tỏa ra khi đốt cháy hoàn toàn 1 kg than đá là:
\(Q=q.m=1,{{25.10}^{7}}.1=1,{{25.10}^{7}}\) J.
d) SAI
Khối lượng than đá cần đốt cháy hoàn toàn để có năng lượng tỏa ra tương đương năng lượng tỏa ra của phản ứng hạt nhân trên khi tổng hợp được 1g He là:
\({{Q}_{t}}=E.N\) \(q.m=E.N\) \(m=\dfrac{E.N}{q}=\dfrac{17,{{6.10}^{6}}.1,{{6.10}^{-19}}.1,{{5.10}^{23}}}{1,{{25.10}^{7}}}=33792\) kg \(\approx 34\) tấn.

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Vật Lí Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
ĐĂNG KÝ GÓI THI VIP
- Truy cập hơn 100K đề thi thử và chính thức các năm
- 2M câu hỏi theo các mức độ: Nhận biết – Thông hiểu – Vận dụng
- Học nhanh với 10K Flashcard Tiếng Anh theo bộ sách và chủ đề
- Đầy đủ: Mầm non – Phổ thông (K12) – Đại học – Người đi làm
- Tải toàn bộ tài liệu trên TaiLieu.VN
- Loại bỏ quảng cáo để tăng khả năng tập trung ôn luyện
- Tặng 15 ngày khi đăng ký gói 3 tháng, 30 ngày với gói 6 tháng và 60 ngày với gói 12 tháng.