Câu hỏi:
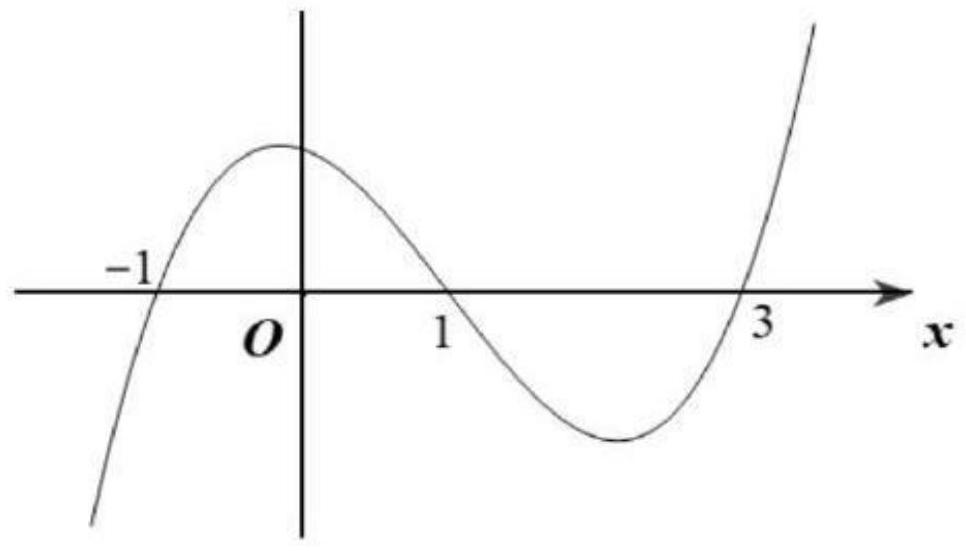
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
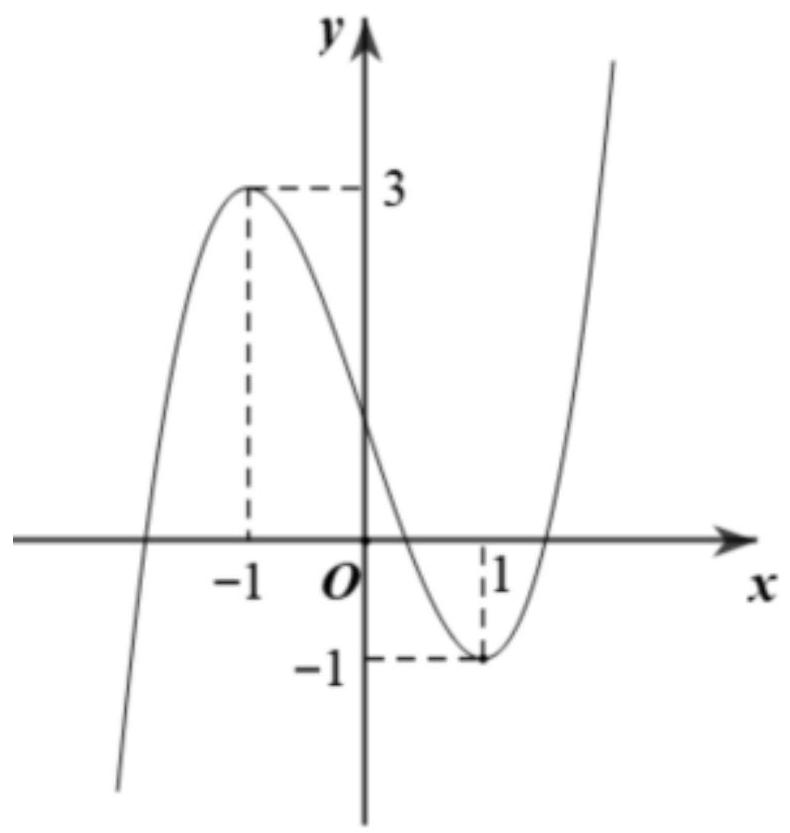
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f(\sin x)=m\) có nghiệm thuộc khoảng \((0 ; \pi)\) ?
Trả lời:
Đáp án đúng: 2
Đặt \(t=\sin x ; \forall x \in(0 ; \pi) \Rightarrow t \in(0 ; 1]\).
Khi đó, phương trình trở thành \(f(t)=m\). Dựa vào đồ thị hàm số ta suy ra \(m \in[-1 ; 1)\).
Mà \(m \in \mathbb{Z}\) nên \(m \in\{-1 ; 0\}\).
Vậy có 2 giá trị nguyên của tham số \(m\) thỏa mãn.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
28/05/2025
0 lượt thi
0 / 50
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT