Câu hỏi:
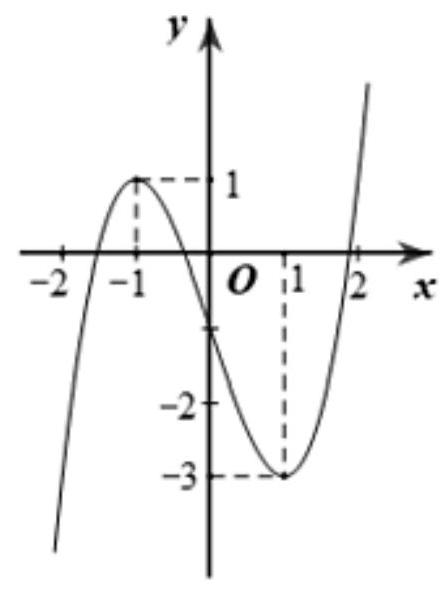
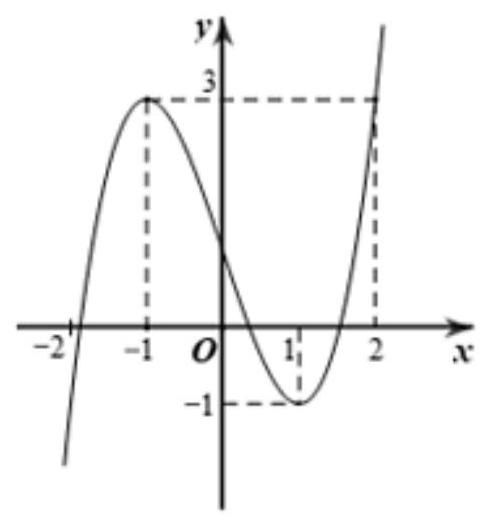
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Số nghiệm thực của phương trình \(|f(x)-1|=3\) bằng
Trả lời:
Đáp án đúng: D
Ta có \(|f(x)-1|=3 \Leftrightarrow\left[\begin{array}{l}f(x)-1=3 \\ f(x)-1=-3\end{array} \Leftrightarrow\left[\begin{array}{l}f(x)=4 \\ f(x)=-2\end{array}\right.\right.\).
Số nghiệm của phương trình \(|f(x)-1|=3\) là số giao điểm của đồ thị hàm số \(y=f(x)\) với hai đường thẳng \(y=4, y=-2\).
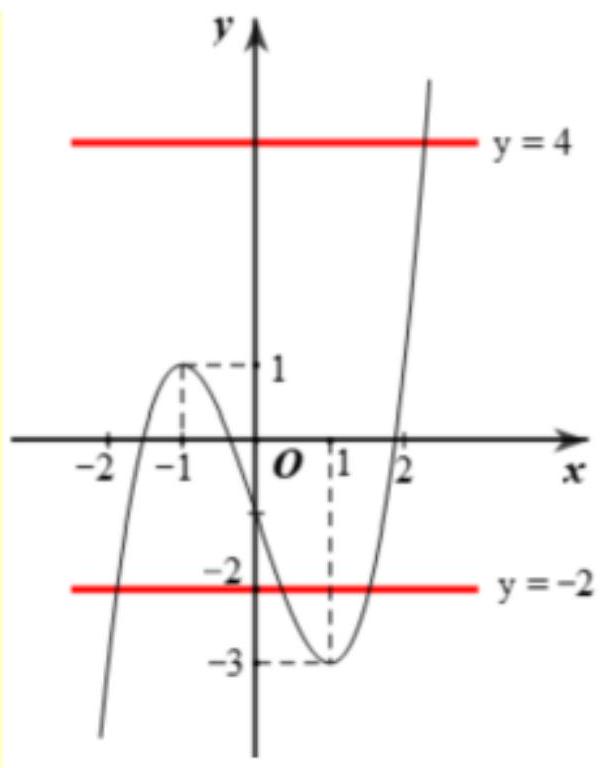
Dựa vào đồ thị hàm số ta có: \(f(x)=4\) có 1 nghiệm, \(f(x)=-2\) có 3 nghiệm. Vậy số nghiệm thực của phương trình \(|f(x)-1|=3\) là 4.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
28/05/2025
0 lượt thi
0 / 50
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

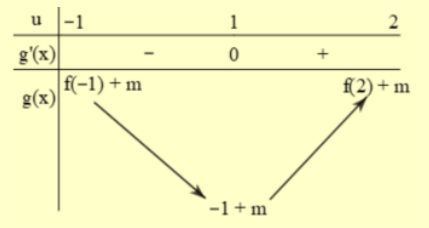
 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)