Cho sơ đồ PERT của một dự án:

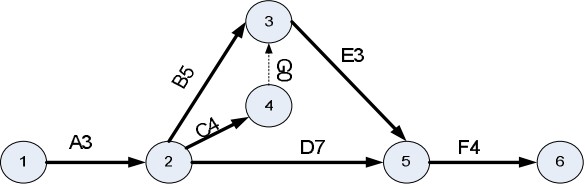
Biết thời gian dự tính ngắn nhất của từng công việc (tn): A=3; B=2; C=2; D=6; E=2; F=4 tuần lễ và chi phí để rút ngắn thời gian xuống 1 tuần lễ của từng công việc là: B=50; C=50; D=30; E=100 triệu đồng. Nếu rút ngắn thời gian của tiến trình tới hạn xuống còn 13 tuần. Lúc này  sẽ xuất hiện những tiến trình tới hạn mới. Trong đó có 01 tiến trình tới hạn với nhiều công việc nhất. Phương án rút ngắn tiến trình tới hạn này có chi phí thấp nhất là:

Để giải quyết bài toán này, ta cần thực hiện các bước sau: 1. **Xác định tiến trình tới hạn ban đầu:** Tiến trình tới hạn là đường đi dài nhất qua sơ đồ PERT. Trong trường hợp này, có hai tiến trình: - A-D-F: 3 + 6 + 4 = 13 tuần - A-E: Không phải tiến trình tới hạn vì tổng thời gian ngắn hơn - B-C: Không phải tiến trình tới hạn vì tổng thời gian ngắn hơn - A-D-E-F: Không phải tiến trình tới hạn vì tổng thời gian ngắn hơn. Như vậy, tiến trình tới hạn ban đầu là A-D-F với thời gian là 13 tuần. 2. **Rút ngắn tiến trình tới hạn:** Yêu cầu là rút ngắn tiến trình tới hạn xuống còn 13 tuần, điều này không cần rút ngắn gì cả. Tuy nhiên, có vẻ như có một lỗi sai trong câu hỏi, câu hỏi có thể muốn rút ngắn tiến trình tới hạn xuống dưới 13 tuần. Nếu ta tiếp tục với giả định rằng đề bài có nghĩa là rút ngắn xuống dưới 13 tuần, ví dụ 12 tuần. 3. **Xác định chi phí rút ngắn:** Ta cần xem xét chi phí để rút ngắn các công việc trên tiến trình tới hạn A-D-F: - Rút ngắn công việc D: Chi phí 30 triệu đồng/tuần. - Các công việc A và F không có chi phí rút ngắn được cung cấp, nên ta không thể rút ngắn chúng. Vì vậy, phương án rút ngắn tiến trình tới hạn với chi phí thấp nhất là rút ngắn công việc D với chi phí 30 triệu đồng/tuần. Tuy nhiên, nếu chúng ta rút ngắn D, lúc này cần xét các tiến trình khác có thể trở thành tiến trình tới hạn mới. 4. **Xét các tiến trình tới hạn mới:** - A-D-F (sau khi rút ngắn D): Nếu rút ngắn D đi 1 tuần thì A-D-F = 12 tuần - A-E-F = 3 + 2 + 4 = 9 tuần. - B-C = 2 + 2 = 4 tuần. Sau khi rút ngắn D, A-D-F vẫn là tiến trình tới hạn. Theo như đề bài, cần tìm phương án rút ngắn tiến trình tới hạn có nhiều công việc nhất, tức là A-D-F (3 công việc) với chi phí thấp nhất là rút ngắn D (30 triệu).