Câu hỏi:
Cho tam giác \(A B C\). Dựng bên ngoài tam giác đó hai tam giác \(A B D, A C E\) vuông cân tại đỉnh \(A\) rồi dựng hình bình hành \(A E I D\). Biết \(\widehat{D A I}=\widehat{A B C}\). Gọi \(K\) là trung điểm của \(B D\).
Đáp án đúng: Sai, Đúng, Đúng, Sai
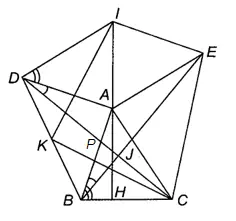
a) Giả sử \(A I\) cắt \(B C\) ở \(H\).
Ta có: \(\widehat{D A I}+\widehat{D A B}+\widehat{B A H}=180^{\circ}\), mà \(\widehat{D A B}=90^{\circ}\) (do \(\triangle D A B\) vuông cân tại \(A\) ).
Suy ra \(\widehat{D A I}+\widehat{B A H}=90^{\circ}\).
b) Ta có \(\widehat{D A I}=\widehat{A B C}\) (gt) nên \(\widehat{A B H}+\widehat{B A H}=90^{\circ}\).
Trong \(\triangle A B H\) có: \(\widehat{A B H}+\widehat{B A H}+\widehat{A H B}=180^{\circ}\).
Suy ra \(\widehat{A H B}=180^{\circ}(\widehat{A B H}+\widehat{B A H})=180^{\circ}-90^{\circ}=90^{\circ}\) hay \(A I \perp B C\).
c) Ta có \(\widehat{B A E}=\widehat{B A C}+\widehat{C A E}=\widehat{B A C}+90^{\circ}\) và \(\widehat{D A C}=\widehat{B A C}+\widehat{B A D}=\widehat{B A C}+90^{\circ}\).
Do đó \(\widehat{B A E}=\widehat{D A C}\).
Xét \(\triangle B A E\) và \(\triangle D A C\) có:
\(A B=A D ; \widehat{B A E}=\widehat{D A C} ; A C=A E ;\)
Do đó \(\triangle B A E=\triangle D A C\) (c.g.c).
Suy ra \(\widehat{E B A}=\widehat{C D A}\) (hai góc tương ứng).
d) Tam giác \(A B D\) vuông cân tại \(A\) nên \(A K\) vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó \(\widehat{D A K}=\frac{1}{2} \widehat{B A D}=45^{\circ}\).
Khi đó \(\widehat{A B K}=\widehat{B A K}=45^{\circ}\) nên \(\Delta A B K\) vuông cân tại \(K\), do đó \(K A=K B\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I – Toán 8 – Chân Trời Sáng Tạo – Bộ Đề 01 tổng hợp các đề kiểm tra học kì I môn Toán lớp 8 theo chương trình Chân Trời Sáng Tạo. Bộ đề giúp học sinh ôn luyện toàn diện các dạng bài trọng tâm như biểu thức đại số, phân thức, phương trình, hệ thức trong tam giác, hình học, đồng thời rèn luyện tư duy logic và kỹ năng giải bài tập hiệu quả để đạt kết quả cao trong kỳ thi học kỳ.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026




