Câu hỏi:
Cho hàm số \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\) là \(f^{\prime}(x)=(x+3)(x-4)\). Tính tổng các giá trị nguyên của tham số \(m \in[-10 ; 5]\) để hàm số : \(y=f\left(x^{2}-3 x+m\right)\) có nhiều điểm cực trị nhất
Đáp án đúng: B
Xét hàm số \(y=f\left(x^{2}-3 x+m\right)\) có
\(y^{\prime}=(2 x-3) \cdot f^{\prime}\left(x^{2}-3 x+m\right)\)
\(y^{\prime}=0\Leftrightarrow\left[\begin{array}{l}2 x-3=0\\ f^{\prime}\left(x^{2}-3 x+m\right)=0\end{array}\right.\)
Để hàm số \(y=f\left(x^{2}-3 x+m\right)\) có nhiều cực trị nhất thì phương trình \(f^{\prime}\left(x^{2}-3 x+m\right)=0\) có nhiều nghiệm bội lẻ khác \(\frac{3}{2}\) nhất.
Xét phương trình: \(f^{\prime}\left(x^{2}-3 x+m\right)=0 \Leftrightarrow\left(x^{2}-3 x+m+3\right)\left(x^{2}-3 x+m-4\right)=0\)
\(\Rightarrow\left[\begin{array}{l}x^{2}-3 x=-m-3 \\ x^{2}-3 x=4-m\end{array}\right.\)
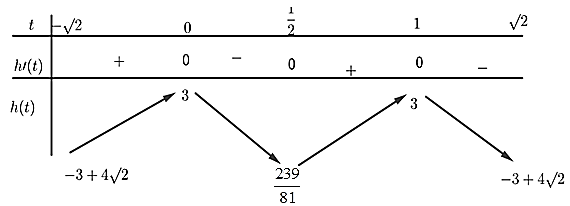
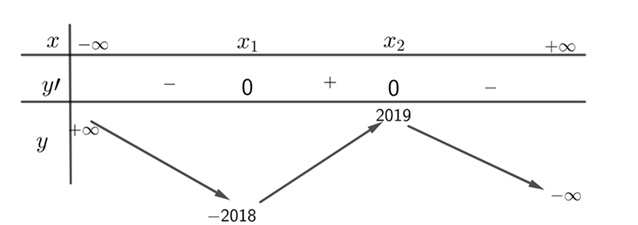
Xét hàm số : \(h(x)=x^{2}-3 x\)
\(h^{\prime}(x)=2 x-3, h^{\prime}=0 \Rightarrow x=\frac{3}{2}\)
Bảng biến thiên hàm số \(h(x)=x^{2}-3 x\)

Để \(f^{\prime}\left(x^{2}-3 x+m\right)=0 \Leftrightarrow\left(x^{2}-3 x+m+3\right)\left(x^{2}-3 x+m-4\right)=0\) có nhiều nghiệm bội lẻ nhất \(\Rightarrow\left[\begin{array}{l}x^{2}-3 x=-m-3 \\ x^{2}-3 x=4-m\end{array}\right.\) có nhiều nghiệm bội lẻ nhất.
Số nghiệm của hai phương trình này là số giao điểm của đồ thị hàm số \(h(x)=x^{2}-3 x\) và các đường thẳng \(y=-m-3\) và \(y=4-m\)
Dựa vào bảng biến thiên của hàm số \(h(x)=x^{2}-3 x \Rightarrow\left[\begin{array}{c}-m-3>\frac{-9}{4} \\ 4-m>\frac{-9}{4}\end{array}\Leftrightarrow\left[\begin{array}{c}m<\frac{-3}{4} \\ m<\frac{25}{4}\end{array}\right.\right.\)
Mà \(m \in[-10 ; 5]\), kết hợp các điều kiện \(\Rightarrow m \in\left(\frac{-3}{4} ; 5\right], m \in \mathbb{Z} \Rightarrow m \in\{0 ; 1 ; 2 ; 3 ; 4 ; 5\}\)
Vậy tổng các giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán là: 15
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Thi Tham Khảo Đánh Giá Năng Lực Năm 2025 – ĐHQG Hà Nội – Đề Số 05 là tài liệu luyện thi toàn diện, giúp học sinh làm quen với cấu trúc và độ khó của kỳ thi ĐGNL theo chuẩn mới. Bộ test gồm đầy đủ 3 phần: Toán học và Xử lý số liệu, Văn học – Ngôn ngữ, và Khoa học/Tiếng Anh, được thiết kế với thời lượng, số câu hỏi và thang điểm đúng theo đề thi chính thức. Các câu hỏi trong bộ test không chỉ kiểm tra kiến thức mà còn rèn luyện tư duy phản biện, lập luận logic và khả năng vận dụng thực tiễn. Đây là tài liệu quan trọng giúp thí sinh tự đánh giá năng lực, luyện tốc độ, nâng cao kỹ năng giải đề và chuẩn bị vững vàng cho kỳ thi Đánh Giá Năng Lực năm 2025 của ĐHQG Hà Nội.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026