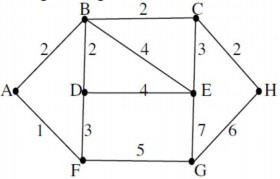
Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại trong đồ thị sau. Đỉnh E được gán trọng số nhỏ nhất là?

Để tìm đường đi ngắn nhất từ đỉnh A đến đỉnh E, ta sử dụng thuật toán Dijkstra. Dưới đây là các bước thực hiện thuật toán Dijkstra trên đồ thị đã cho:

Khởi tạo:

• Khoảng cách từ A đến A là 0, khoảng cách đến các đỉnh còn lại là vô cùng.
• Tập các đỉnh chưa xét: {A, B, C, D, E}.

Lặp:

1. Chọn đỉnh có khoảng cách nhỏ nhất từ A trong tập các đỉnh chưa xét. Ban đầu, đỉnh A được chọn.
2. Cập nhật khoảng cách từ A đến các đỉnh lân cận của A (B và C):
3. A -> B: Khoảng cách là 2.
4. A -> C: Khoảng cách là 4.
5. Loại A khỏi tập các đỉnh chưa xét.
6. Chọn đỉnh có khoảng cách nhỏ nhất từ A trong tập các đỉnh chưa xét (B và C). Đỉnh B được chọn (khoảng cách là 2).
7. Cập nhật khoảng cách từ A đến các đỉnh lân cận của B (C và D):
8. B -> C: Khoảng cách từ A đến C là min(4, 2 + 1) = 3.
9. B -> D: Khoảng cách từ A đến D là 2 + 7 = 9.
10. Loại B khỏi tập các đỉnh chưa xét.
11. Chọn đỉnh có khoảng cách nhỏ nhất từ A trong tập các đỉnh chưa xét (C, D, E). Đỉnh C được chọn (khoảng cách là 3).
12. Cập nhật khoảng cách từ A đến các đỉnh lân cận của C (D và E):
13. C -> D: Khoảng cách từ A đến D là min(9, 3 + 2) = 5.
14. C -> E: Khoảng cách từ A đến E là 3 + 2 = 5.
15. Loại C khỏi tập các đỉnh chưa xét.
16. Chọn đỉnh có khoảng cách nhỏ nhất từ A trong tập các đỉnh chưa xét (D, E). Cả D và E đều có khoảng cách là 5. Chọn E.
17. Loại E khỏi tập các đỉnh chưa xét.

Vậy, đường đi ngắn nhất từ A đến E là 5.