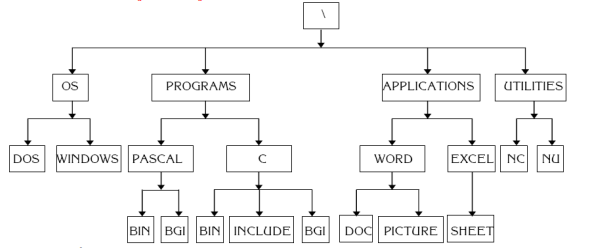
Dùng phương pháp lưu trữ liên tiếp để lưu trữ một ma trận ( mảng hai chiều) có nhược điểm lớn nhất là:

Thuật toán sắp xếp nổi bọt (Bubble Sort) hoạt động bằng cách lặp đi lặp lại qua danh sách, so sánh các cặp phần tử liền kề và hoán đổi chúng nếu chúng không đúng thứ tự. Trong mỗi lần lặp, phần tử lớn nhất "nổi" lên vị trí cuối cùng (hoặc đầu tiên, tùy thuộc vào cách triển khai) của danh sách chưa được sắp xếp.

Phương án 1 mô tả chính xác cách hoạt động của thuật toán Bubble Sort: đi từ cuối mảng về đầu mảng, so sánh các phần tử liền kề và đổi chỗ nếu cần để đưa phần tử lớn hơn "nổi" lên. Sau N-1 lần lặp, mảng sẽ được sắp xếp.

Phương án 2 sai vì Bubble Sort cần N-1 lần lặp, không phải N lần.

Phương án 3 sai vì Bubble Sort cần N-1 lần lặp, không phải N lần.

Phương án 4 sai vì có một đáp án đúng (phương án 1).

Chiều dài đường đi của một cây là tổng độ dài đường đi từ gốc đến tất cả các nút. Trong cây đã cho:
- Nút gốc (8) có độ dài đường đi là 0.
- Các nút con của nút gốc (3, 10) có độ dài đường đi là 1.
- Các nút con của nút 3 (1, 6) có độ dài đường đi là 2.
- Các nút con của nút 10 (4, 7, 14) có độ dài đường đi là 2.
- Nút con của nút 6 (9) có độ dài đường đi là 3.
- Nút con của nút 14 (13) có độ dài đường đi là 3.

Vậy, tổng chiều dài đường đi của cây là:
(1 * 2) + (2 * 5) + (3 * 2) = 2 + 10 + 6 = 18. Đây là tổng số cạnh trên tất cả các đường đi từ gốc đến mỗi nút.

Tuy nhiên, câu hỏi có vẻ như đang yêu cầu tổng của các giá trị trên mỗi đường đi, chứ không phải tổng số cạnh. Vậy ta tính lại như sau:

Đường đi từ gốc (8) đến các nút:
- 8 -> 3: 8 + 3 = 11
- 8 -> 10: 8 + 10 = 18
- 8 -> 3 -> 1: 8 + 3 + 1 = 12
- 8 -> 3 -> 6: 8 + 3 + 6 = 17
- 8 -> 10 -> 4: 8 + 10 + 4 = 22
- 8 -> 10 -> 7: 8 + 10 + 7 = 25
- 8 -> 10 -> 14: 8 + 10 + 14 = 32
- 8 -> 3 -> 6 -> 9: 8 + 3 + 6 + 9 = 26
- 8 -> 10 -> 14 -> 13: 8 + 10 + 14 + 13 = 45

Tổng chiều dài đường đi = 11 + 18 + 12 + 17 + 22 + 25 + 32 + 26 + 45 = 208

Nhưng đây không phải là đáp án có sẵn. Có vẻ như câu hỏi yêu cầu tổng khoảng cách từ mỗi nút đến tất cả các nút khác. Điều này phức tạp hơn nhiều.

Một cách hiểu khác, và có lẽ là cách hiểu đúng nhất, là tính tổng độ dài đường đi từ gốc đến mỗi nút, trong đó độ dài đường đi là số cạnh (edges) trên đường đi đó.

- Nút 3 và 10 có độ dài đường đi là 1.
- Nút 1, 6, 4, 7, 14 có độ dài đường đi là 2.
- Nút 9 và 13 có độ dài đường đi là 3.

Tổng độ dài đường đi = (1 * 2) + (2 * 5) + (3 * 2) = 2 + 10 + 6 = 18

Tuy nhiên, các đáp án đều lớn hơn nhiều. Có lẽ đề bài muốn tính tổng *các giá trị* của các nút trên đường đi từ gốc đến mỗi nút.

Tính lại theo cách này:
- 8 -> 3 = 11
- 8 -> 10 = 18
- 8 -> 3 -> 1 = 12
- 8 -> 3 -> 6 = 17
- 8 -> 10 -> 4 = 22
- 8 -> 10 -> 7 = 25
- 8 -> 10 -> 14 = 32
- 8 -> 3 -> 6 -> 9 = 26
- 8 -> 10 -> 14 -> 13 = 45

Tổng = 11 + 18 + 12 + 17 + 22 + 25 + 32 + 26 + 45 = 208

Có vẻ như không có đáp án nào đúng với các cách hiểu thông thường về "chiều dài đường đi" của cây. Tuy nhiên, nếu ta cộng *giá trị của tất cả các nút* trong cây, ta có:
8 + 3 + 10 + 1 + 6 + 4 + 7 + 14 + 9 + 13 = 75. Cái này cũng không có trong đáp án.

Do đó, dựa trên các cách hiểu thông thường về chiều dài đường đi của cây và các phép tính đã thực hiện, không có đáp án nào trong số các lựa chọn là chính xác. Câu hỏi có thể bị sai sót hoặc thiếu thông tin.

Khi một hàng đợi (queue) đã trải qua các thao tác thêm (enqueue) và loại bỏ (dequeue) phần tử, và hiện tại đang ở trạng thái rỗng, điều này có nghĩa là các phần tử đã được thêm vào trước đó đều đã được lấy ra hết. Trong cấu trúc hàng đợi sử dụng mảng hoặc danh sách liên kết, thông thường, chúng ta sử dụng hai biến (hoặc con trỏ) là `front` (lối trước) và `rear` (lối sau) để theo dõi vị trí của phần tử đầu tiên và phần tử cuối cùng trong hàng đợi.

Khi hàng đợi rỗng, có hai trường hợp xảy ra:
1. Hàng đợi rỗng ngay từ đầu: Cả `front` và `rear` đều được khởi tạo là một giá trị đặc biệt (thường là 0 hoặc -1) để biểu thị hàng đợi rỗng.
2. Hàng đợi rỗng sau khi thực hiện các thao tác: Sau khi thêm và loại bỏ các phần tử, nếu số lượng phần tử được loại bỏ bằng số lượng phần tử đã thêm vào, hàng đợi sẽ trở về trạng thái rỗng. Trong trường hợp này, `front` và `rear` có thể trở về giá trị ban đầu (ví dụ: 0) hoặc có thể bằng nhau tại một vị trí nào đó trong mảng/danh sách, tùy thuộc vào cách cài đặt.

Phương án 4, "Lối trước nhận giá trị = 0", là phù hợp nhất vì nó thể hiện trạng thái ban đầu hoặc trạng thái sau khi các phần tử đã được loại bỏ hết và `front` quay trở về giá trị khởi tạo ban đầu là 0 (hoặc một giá trị tương đương tùy vào cách cài đặt). Các phương án khác không mô tả chính xác trạng thái rỗng của hàng đợi sau các thao tác thêm và loại bỏ.