Câu hỏi:
Vòng năng lượng theo vòng tuần hoàn của nước có sự chuyển hóa năng lượng mặt trời thành các dạng năng lượng.
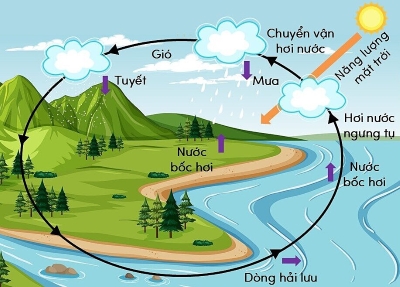
Vòng năng lượng theo vòng tuần hoàn của nước trải qua mấy giai đoạn?
Đáp án đúng: 3
Vòng năng lượng theo vòng tuần hoàn của nước trải qua ba giai đoạn chính:
- Bốc hơi: Nước từ bề mặt các đại dương, sông hồ, và đất hấp thụ năng lượng từ mặt trời và chuyển từ thể lỏng thành thể khí (hơi nước). Quá trình này thu năng lượng từ Mặt Trời.
- Ngưng tụ: Khi hơi nước lên cao gặp nhiệt độ lạnh hơn, nó ngưng tụ lại thành các giọt nước và hình thành mây. Trong quá trình này, năng lượng được giải phóng ra môi trường.
- Mưa: Khi mây chứa đủ nước, nước sẽ rơi xuống mặt đất dưới dạng mưa, tuyết hoặc mưa đá, cung cấp nước cho sông hồ, đất đai và các nguồn nước khác.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Kiểm Tra Học Kì I - Khoa Học Tự Nhiên 9 - Kết Nối Tri Thức là một bài kiểm tra toàn diện giúp các em học sinh tổng kết và củng cố kiến thức đã học. Đề thi bao gồm nhiều dạng bài tập giúp các em rèn luyện kỹ năng làm bài và phát triển tư duy giải quyết vấn đề một cách khoa học.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026