Trắc nghiệm Cộng, trừ và nhân số phức Toán Lớp 12

Câu 1:

Gọi \(z_1;z_2\)  là hai nghiệm phức của phương trình \(z^{2}-z+1=0\). Giá trị của \(\left|z_{1}\right|+\left|z_{2}\right|\) bằng.

Câu 2:

Kí hiệu \(z_{1}, z_{2}\) lần lượt là hai nghiệm phức của phương trình \(2 z^{2}-2 z+5=0\) . Giá trị của biểu thức

Câu 3:

Gọi \(z_1;z_2\) , là hai nghiệm phức của phương trình \(z^{2}+2 \sqrt{2} z+8=0\) . Tính giá trị của biểu thức \(T=\left|z_{1}^{4}\right|+\left|z_{2}^{4}\right|\)
 

Câu 4:

Gọi z₁ và z₂ lần lượt là nghiệm của phương trình: \(z^{2}+2 z+5=0\). Tính \(F=\left|z_{1}\right|+\left|z_{2}\right|\)

Câu 5:

Gọi z₁ , z₂ là hai nghiệm phức của phương trình \(5 z^{2}-8 z+5=0\) \(S=\left|z_{1}\right|+\left|z_{2}\right|+z_{1} z_{2}\)

Câu 6:

Gọi \(z_{1}, z_{2}\) 2 , là hai nghiệm phức của phương trình \(2 z^{2}-3 z+7=0\) . Tính giá trị của biểu thức \(P=\left|z_{1}\right|+\left|z_{2}\right|\)

Câu 7:

Cho các số phức \(z_{1} \neq 0, z_{2} \neq 0\) thỏa mãn điều kiện \(\frac{2}{z_{1}}+\frac{1}{z_{2}}=\frac{1}{z_{1}+z_{2}}\) Tính giá trị của biểu thức \(P=\left|\frac{z_{1}}{z_{2}}\right|+\left|\frac{z_{2}}{z_{1}}\right|\)
 

Câu 8:

Gọi z₁ , z₂ là các nghiệm phức của phương trình \(z^{2}-4 z+5=0\) . Giá trị của \(\left(z_{1}-1\right)^{2018}+\left(z_{2}-1\right)^{2018}\) bằng

Câu 9:

Gọi z₁ và z₂ là hai nghiệm phức của phương trình: \(z^{2}+4 z+7=0\) . Khi đó \(\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\) bằng:

Câu 10:

Cho phương trình \(z^{2}-2 z+3=0\) trên tập số phức, có hai nghiệm là z₁ , z₂ . Khi đó \(\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\) có giá trị là :
 

Câu 11:

Gọi z₁ và z₂ lần lượt là hai nghiệm của phương trình \(z^{2}-4 z+5=0\) . Giá trị của biểu thức \(P=\left(z_{1}-2 z_{2}\right) \cdot \overline{z_{2}}-4 z_{1}\)

Câu 12:

Cho phương trình \(z^{2}+2 z+10=0\) . Gọi z₁ và z₂ là hai nghiệm phức của phương trình đã cho. Khi đó giá trị biểu thức \(A=\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\) bằng: 

Câu 13:

Phương trình \(z^{2}-2 z+6=0\) có các nghiệm z₁ ; z₂ . Khi đó giá trị của biểu thức \(M=\frac{z_{1}^{2}}{z_{1}^{2}}+\frac{z_{2}^{2}}{z_{2}^{2}}\) là:
 

Câu 14:

Gọi z₁ , z₂ là các nghiệm phức của phương trình \(z^{2}+4 z+5=0\) . Đặt \(w=\left(1+z_{1}\right)^{100}+\left(1+z_{2}\right)^{100}\) . Khi đó

Câu 15:

Phương trình \(x^{2}+4 x+5=0\) có nghiệm phức mà tổng các mô đun của chúng bằng?

Câu 16:

Cho \(z_1;z_2\) là hai nghiệm của phương trình \(z^{2}+2 z+3=0\). Tính \(\left|z_{1}\right|+\left|z_{2}\right|\)

Câu 17:

Trong tập các số phức z₁ , z₂ lần lượt là 2 nghiệm của phương trình \(z^{2}+4 z+5=0\) . Tính \(P=\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\)

Câu 18:

Cho z₁ , z₂ là hai nghiệm của phương trình \(z^{2}-2 z+2=0 \quad(z \in \mathbb{C})\). Tính giá trị của biểu thức \(P=2\left|z_{1}+z_{2}\right|+\left|z_{1}-z_{2}\right|\)

Câu 19:

Gọi z₁ và z₂ là các nghiệm của phương trình \(z^{2}-4 z+9=0\) . Gọi M , N là các điểm biểu diễn của z₁ và z₂ trên mặt phẳng phức. Khi đó độ dài của MN là

Câu 20:

Gọi \(z_1;z_2\) , là hai nghiệm phức của phương trình \(z^{2}-4 z+9=0\) Tổng \(P=\left|z_{1}\right|+\left|z_{2}\right|\) bằng:

Câu 21:

Gọi z₁ và z₂ là hai nghiệm phức của phương trình \(z^{2}+2 z+10=0\) , giá trị của biểu thức \(A=\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\) là.

Câu 22:

Gọi z₁ , z₂ là hai nghiệm phức của phương trình \(z^{2}-4 z+5=0\) . Giá trị của biểu thức \(\left|z_{1}^{2}\right|+\left|z_{2}^{2}\right|\) bằng.

Câu 23:

Gọi \(z_1; z_2\) , là hai nghiệm phức của phương trình \(2 z^{2}+4 z+3=0\) . Tính giá trị của biểu thức \(\left|z_{1}\right|+\left|z_{2}\right|\)

Câu 24:

Cho \(z_1; z_2\) , là các nghiệm phức của phương trình \(z^{2}+4 z+13=0\) . Tính \(m=\left|\left(z_{1}-2\right)^{2}\right|+\left|\left(z_{2}-2\right)^{2}\right|\)

Câu 25:

Phương trình (1+2i)x = 3x-i cho ta nghiệm:

Câu 26:

Số nào sau đây bằng số (2-i)(3+4i)?

Câu 27:

Xét các kết quả sau:

(1) \({i^3} = i\)

(2) \({i^4} = i\)

(3) \({\left( {1 + i} \right)^3} =  - 2 + 2i\)

Trong ba kết quả trên, kết quả nào sai?

Câu 28:

Tìm phần ảo của số phức z, biết \(\bar z = {\left( {\sqrt 2  + i} \right)^2}\left( {1 - \sqrt 2 i} \right)\)

Câu 29:

Cho số phức \({z_1} = 2 + 3i,\;{z_2} =  - 4 - 5i\). Tính \(\;z = {z_1} + {z_2}.\)

Câu 30:

Cho số phức \(z = a + bi\left( {a,b \in } \right)\) thỏa mãn \(z + 1 + 3i - \left| z \right|i = 0\)

Tính S = a+3b.

Câu 31:

Cho số phức \(z = 1 - \frac{1}{3}i\). Tìm số phức \(w = \overline {iz}  + 3z\) được

Câu 32:

Cho số phức z thỏa mãn \(\left( {1 + 3i} \right)z - 5 = 7i\)

Mệnh đề nào sau đây là mệnh đề đúng?

Câu 33:

Điểm A trong hình vẽ bên dưới biểu diễn cho số phức z.

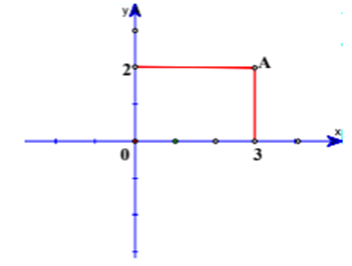
Mệnh đề nào sau đây đúng?

Câu 34:

Cho số phức \(z = {\left( {1 - 2i} \right)^2}\), số phức liên hợp của z là

Câu 35:

Cho hai số thực x, y thỏa mãn phương trình \(x\; + \;2i\; = 3\; + \;4yi\). Khi đó, giá trị của x và y là:

Câu 36:

Số phức z = (1−i)³ bằng

Câu 37:

Số phức z=(1+i)² bằng

Câu 38:

Tích của hai số phức z₁ = 3 + 2i, z₂ = 2 − 3i là

Câu 39:

Cho hai số phức z₁ = 2 + 3i, z₂ = 2 − 4i . Hiệu z₁ − z₂ bằng

Câu 40:

Tổng của hai số phức z₁ = 1 − 2i, z₂ = 2 − 3i là

Câu 41:

Giá trị của i¹⁰⁵+ i²³+ i²⁰- i³⁴ là ?

Câu 42:

Giá trị của biểu thức S = 1+ i²+ i⁴+ ...+ i^4k là

Câu 43:

Tìm số phức liên hợp của số phức \(z = \frac{{1 + i}}{{2 - i}}\)

Câu 44:

Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức \(w = iz + \overline z \)

Câu 45:

Cho số phức \(\overline z  = 3 + 2i\). Tìm số phức \(w = 2i\overline z  + z\)

Câu 46:

Cho số phức z = 6 - 8i. Tìm số phức \(w = iz - \overline z \)

Câu 47:

Tìm số phức \(z = \frac{{3 - 4i}}{{4 - i}}\)

Câu 48:

Cho hai số phức z1 = 1 + i; z2 = 4 - i. Tim số phức \(z = z_1^2.{z_2}\)

Câu 49:

Cho hai số phức z₁ = 1 + i; z₂ = 1 - 2i. Tìm số phức z = z₁.z₂.

Câu 50:

Cho hai số phức z = i. Tìm số phức w = z⁵.