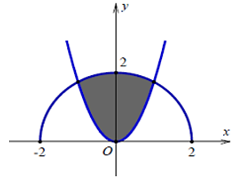
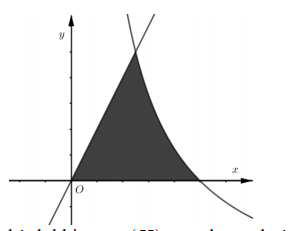
Gọi (H) là hình phẳng được giới hạn bởi các đồ thị hàm số \(y=2 x, y=\frac{1-x}{x}, y=0\) (phần tô đậm màu đen ở hình vẽ bên).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình hoành độ giao điểm của \(y=2 x \text { và } y=\frac{1-x}{x}\) là:
\(2 x=\frac{1-x}{x} \Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ 2 x^{2}+x-1=0 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ {\left[\begin{array}{l} x=\frac{1}{2} \\ x=-1 \end{array}\right.} \end{array} \Leftrightarrow x=\frac{1}{2}\right.\)
Phương trình hoành độ giao điểm của \(y=2 x\, và \,y=0\) là:
\(2 x=0 \Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ 2 x^{2}+x-1=0 \end{array} \Leftrightarrow x=0\right.\)
Phương trình hoành độ giao điểm của \(y=0 \text { và } y=\frac{1-x}{x}\) là:
\(\frac{1-x}{x}=0 \Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ 1-x=0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ x=1 \end{array} \Leftrightarrow x=1\right.\right.\)
Khi đó:
\(V=\pi \int\limits_{0}^{\frac{1}{2}} 4 x^{2} \mathrm{d} x+\pi \int\limits_{\frac{1}{2}}^{1}\left(\frac{1-x}{x}\right)^{2} \mathrm{d} x=\left.\pi \cdot \frac{4 x^{3}}{3}\right|_{0} ^{\frac{1}{2}}+\pi \int\limits_{\frac{1}{2}}^{1}\left(\frac{1}{x}-1\right)^{2} \mathrm{d} x=\frac{1}{6} \pi+\pi \int\limits_{\frac{1}{2}}^{1}\left(\frac{1}{x^{2}}-\frac{2}{x}+1\right) \mathrm{d} x\)
=\(\frac{1}{6} \pi+\pi\left[\left.\left(-\frac{1}{x}\right)\right|_{\frac{1}{2}} ^{1}-\left.2 \ln x\right|_{\frac{1}{2}} ^{1}+\left.x\right|_{\frac{1}{2}} ^{1}\right]\)
\(\begin{array}{l} =\frac{1}{6} \pi+\pi\left[-1+2-2 \ln 2+\frac{1}{2}\right] \\ =\frac{1}{6} \pi+\frac{3}{2} \pi-2 \pi \ln 2 \\ =\frac{10}{6} \pi-2 \pi \ln 2=\pi\left(\frac{5}{3}-2 \ln 2\right) \end{array}\)
Câu hỏi liên quan
-
Cho (H) là hình phẳng giới hạn bởi parabol \(y=\sqrt 3 {x^2}\) và nửa đường tròn có phương trình \(y=\sqrt {4\; - {x^2}} \) với −2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
-
Tìm mệnh đề đúng trong các mệnh đề sau:
-
Biết \(I = \int_0^\pi {\frac{{x{{\sin }^{2020}}x}}{{{{\sin }^{2020}}x + {{\cos }^{2020}}x}}} {\rm{d}}x = \frac{{{\pi ^a}}}{b} + c,\,\,\left( {a,b,c \in {\mathbb{Z}^ + }} \right).\) Tính P = a.b.c
-
Giá trị của tích phân \(I=\int_{0}^{1} \frac{\ln (1+x)}{1+x^{2}} d x\) là
-
Tính tích phân sau \(B = \mathop \smallint \nolimits_0^1 {x^3}{\left( {{x^4} - 1} \right)^5}dx\)
-
Tích phân \(I=\int_{1}^{\sqrt[4]{3}} \frac{1}{x\left(x^{4}+1\right)} d x\) bằng
-
Cho \(\int\limits_1^2 {f\left( x \right){\rm{d}}x} = 3, \int\limits_0^2 {f\left( {5x + 2} \right){\rm{d}}x} = 3\). Khi đó \(\int\limits_1^{12} {f\left( x \right){\rm{d}}x} \) bằng
-
Nếu \(\int_{1}^{3}[f(x)-2 x] \mathrm{d} x=5 \text { thì } \int_{1}^{3} f(x) \mathrm{d} x \text { bằng }\)
-
Cho a là một số dương lớn hơn 1. Mệnh đề nào dưới đây sai?
-
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=-x^{2}+4\) , đường thẳng x = 3 , trục tung và trục hoành là
-
Cho hàm số \(f(x) = \left\{ \begin{array}{l} {x^3} + x + 2\,\,\,{\rm{khi }}x < 1\\ x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi }}x \ge 1 \end{array} \right.\). Tính tích phân \(\int\limits_{0}^{\frac{\pi }{2}}{f\left( 3{{\sin }^{2}}x-1 \right)}\sin 2x\text{d}x\).
-
Cho \(\mathop \smallint \nolimits_1^2 f\left( {{x^2} + 1} \right)xdx\; = \;2\;\). Khi đó \(\mathop \smallint \nolimits_2^5 f\left( x \right)dx\) bằng
-
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) thoả \(f\left( {{x}^{5}}+4x+3 \right)=2x+1,\,\forall x\in \mathbb{R}.\)tích phân \(\int_{-2}^{8}{f\left( x \right)}dx\) bằng
-
Cho hàm số f(x) thỏa mãn
\(f^{\prime}(x)+2 x \cdot f(x)=\mathrm{e}^{x} f(x) \text { với } f(x) \neq 0, \forall x \text { và } f(0)=1\) . Khi đó \(\mid f(1)|\) bằng? -
Cho \(I=\int_{1}^{2} f(x) \mathrm{d} x=2\) . Giá trị của \(J=\int_{0}^{\frac{\pi}{2}} \frac{\sin x \cdot f(\sqrt{3 \cos x+1})}{\sqrt{3 \cos x+1}} \mathrm{~d} x\)
-
Cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgY % da8iaadIhacqGH8aapdaWcaaqaaiabec8aWbqaaiaaikdaaaaaaa!3C3B! 0 < x < \frac{\pi }{2}\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WG4bGaciiDaiaacggacaGGUbGaamiEaiaabsgacaWG4bGaeyypa0da % leaacaaIWaaabaGaamyyaaqdcqGHRiI8aOGaamyBaaaa!42AD! \int\limits_0^a {x\tan x{\rm{d}}x = } m\). Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maapehabaWaaeWaaeaadaWcaaqaaiaadIhaaeaaciGGJbGaai4B % aiaacohacaWG4baaaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaa % aakiaabsgacaWG4baaleaacaaIWaaabaGaamyyaaqdcqGHRiI8aaaa % !450D! I = \int\limits_0^a {{{\left( {\frac{x}{{\cos x}}} \right)}^2}{\rm{d}}x} \) theo a và m
-
Tích phân \(I=\int_{0}^{a} x \sqrt{x+1} d x\) có giá trị:
-
Tích phân \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maapehabaGaamiEaiaac6cacaqGLbWaaWbaaSqabeaacaaIYaGa % amiEaaaakiaabsgacaWG4baaleaacaaIWaaabaGaaGOmaaqdcqGHRi % I8aaaa!4212! I = \int\limits_0^2 {x.{{\rm{e}}^{2x}}{\rm{d}}x} \) là
-
Giá trị của \(\int\limits_0^2 {2{e^{2x}}{\rm{d}}x} \) là:
-
Cho số thực a thỏa mãn \(\int_{-1}^{a} e^{x+1} d x=e^{2}-1\), khi đó a có giá trị bằng
